-
1、已知x=2- , y=2+.(1)、求x2+y2-3xy的值:(2)、若x的小数部分是a,y的整数部分是b,求ax-by的值.
-
2、已知关于的方程 .(1)、若这个方程是一元二次方程,求的值;(2)、若是它的一个根,求的值.
-
3、如果关于x的一元二次方程a2+bx+c=0有两个实数根,且其中一个根为另外一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的有(填序号)
①方程x2-x-2=0是倍根方程;
②若(x-2)(mx+n)=0是倍根方程:则4m2+5mn+n2=0;
③若p,q满足pq=2,则关于x的方程叔px2+3x+q=0是倍根方程;
④若关于x的一元二次方程ax2+bx+c=0是倍根方程,则必有2b2=9ac·
-
4、已知一元二次方程x2+7x-1=0的两个实数根为α,β,则(α-1)(β-1)的值为.
-
5、如图,在一块长为12m,宽为8m的长方形空地上,修建同样宽的两条互相垂直的道路(两条道路各与长方形的一条边平行),剩余部分栽种花草,且栽种花草的面积为77m2 , 则道路的宽为m.
-
6、二次根式是一个整数,那么正整数a的最小值是.
-
7、把方程化成一般形式为.
-
8、关于的一元二次方程的两个根为 , 且 . 下列说法正确是( )
①;②;③④关于x的一元二次方程的两个相头 .
A、①②③ B、①②④ C、③④ D、①③④ -
9、某种流感病毒的传染速度很快,若一人携带病毒未进行有效隔离,经过两轮传染后共有256人患病,求每轮传染中平均每个人传染了几人,设每轮传染中平均每个人传染了x人,则由题意可列出方程( )A、 B、 C、 D、
-
10、关于的一元二次方程的两实数根互为相反数,则的值是( )A、2 B、0 C、 D、-2
-
11、某超市2005年一月份的荌业额为200万元,三月份营业额为288万元,如果每月比上月增长的百分数相同,则平均每月的增长率是( )A、 B、 C、 D、
-
12、若方程中,a、b、c满足和 , 则方程的根是( )A、1,0 B、 C、 D、无法确定
-
13、二次方程的两根为-1和5,则一次函数不经过第( )象限A、一 B、二 C、三 D、四
-
14、二次方程的两根为1和5,则一次函数平经过第( )象限A、一 B、二 C、三 D、四
-
15、下列方程中,一定是一元二次方程的是( )A、 B、 C、 D、
-
16、综合与实践:
问题情境:
如图,直线PQ //MN,一副三角尺(∠ABC=∠CDE=90°,∠ACB=30°,∠BAC=60°,∠DCE=∠DEC=45°)按如图①放置,其中点E在直线PO上,点B,C均在直线MN上,且CE平分∠ACN.

问题解决:
(1)、求∠DEQ的度数.(2)、如图②,若将三角形ABC绕点B以每秒4度的速度逆时针方向旋转(A,C的对应点分别为F,G),设旋转时间为 ((s)(0≤t≤45);①在旋转过程中,若边BG//CD,求t的值;
②若在三角形ABC绕点B旋转的同时,三角形CDE绕点E以每秒3度的速度顺时针方向旋转(C,D的对应点为H. K)请直接写出当边BG//HK时,求r的值
-
17、
设计烟花采购方案
为吸引游客,浦江县决定举办烟花节,需考虑如何采购烟花及烟花燃放时长
素材1
已知购买3箱A型和2箱B型烟花需要600元,购买5箱A型和3箱B型烟花需要950元
素材2
某烟花厂提供产品信息如下:
(1)A型烟花每箱8发,B型烟花每箱12发.
(2)即将推出新品C型烟花,每箱200元,每箱15发
(3)本厂生产的所有型号烟花每发保持5秒,(例如A型烟花燃放时间为40s)
素材3
(1)浦江县准备支出7800元(全部用完)购买烟花.
(2)燃放烟花时逐箱不间断燃放,且每次仅燃放一箱,假设每发烟花均能正常绽放,且间隔时长保持不变,忽略每箱烟花之间的引燃时间
问题解决
任务1
确定订单
求A、B型烟花每箱多少元?
任务2
确定方案①
若仅购买A,B型烟花,可以燃放多少秒?
确定方案②
若同时采购A、B、C三种烟花,A型烟花的箱数是C型的5倍,如何采购使得燃放时间最长?
-
18、如图1是一个长为2m、宽为2n的长方形(m>n),沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
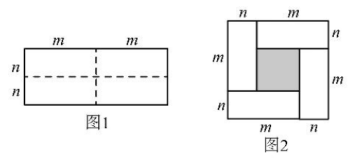 (1)、你认为图2中的阴影部分的正方形的边长等于.(2)、利用你得到的结论解决:m+n=7,mn=12. 求m2+n2 , m-n的值.(3)、如果(2020-m)2+(m-2021)2=7. 求(2020-m)(m-2021) 的值
(1)、你认为图2中的阴影部分的正方形的边长等于.(2)、利用你得到的结论解决:m+n=7,mn=12. 求m2+n2 , m-n的值.(3)、如果(2020-m)2+(m-2021)2=7. 求(2020-m)(m-2021) 的值 -
19、小莹和小亮每人带了16元钱到学校附近的文具店购买中性笔和笔记本,他们要购买的中性笔每盒10支,如果整盒买比单支买每支可优惠0.2元.小莹要买2支中性笔和3本笔记本共需花费14元;小亮要买8支中性笔和2本笔记本共需花费16元.(1)、单独购买一支中性笔多少元?每本笔记本的单价是多少元?(2)、小莹和小亮都还想再买一件单价为1.5元的小工艺品,他们利用所带的钱,能否做到既买全了想要的文具,又都能买到一件小工艺品?请通过运算说明.
-
20、定义一种幂的新运算:xa⊕xb=xab+xa+b , 请利用这种运算规则解决下列问题.(1)、求22⊕23的值;(2)、2P=3,2q=5,3q=6,求2P⊕2q的值;(3)、若运算9⊕32t的结果为810,则t的值是多少?