山东省滨州市无棣县2016-2017学年八年级下学期期末考试数学试题
试卷日期:2017-08-07 考试类型:期末考试
一、选择题
-
1. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列条件中不能确定四边形ABCD是平行四边形的是( )A、AB=CD,AD∥BC B、AB=CD,AB∥CD C、AB∥CD,AD∥BC D、AB=CD,AD=BC3. 在下列的线段中,能组成直角三角形的是 ( )A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,64. 若y=kx-4的函数值y随x的增大而增大,则k的值可能是下列的( )A、-2 B、- C、0 D、25.
2. 下列条件中不能确定四边形ABCD是平行四边形的是( )A、AB=CD,AD∥BC B、AB=CD,AB∥CD C、AB∥CD,AD∥BC D、AB=CD,AD=BC3. 在下列的线段中,能组成直角三角形的是 ( )A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,64. 若y=kx-4的函数值y随x的增大而增大,则k的值可能是下列的( )A、-2 B、- C、0 D、25.如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=10,BC=5,则DE:EC的值( )
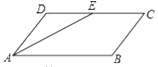 A、1:1 B、1:2 C、2:3 D、3:46. 已知一组数据为:10,8,10,12,10.其中中位数、平均数和众数的大小关系是( )A、众数=中位数=平均数 B、中位数<众数<平均数 C、平均数>中位数>众数 D、平均数<中位数<众数7. 小明的爸爸早晨出去散步,从家走了20分到达距离家800米的公园,他在公园休息了10分,然后用30分原路返回家中,那么小明的爸爸离家的距离S(单位:米)与离家的时间t(单位:分)之间的函数关系图象大致是( )A、
A、1:1 B、1:2 C、2:3 D、3:46. 已知一组数据为:10,8,10,12,10.其中中位数、平均数和众数的大小关系是( )A、众数=中位数=平均数 B、中位数<众数<平均数 C、平均数>中位数>众数 D、平均数<中位数<众数7. 小明的爸爸早晨出去散步,从家走了20分到达距离家800米的公园,他在公园休息了10分,然后用30分原路返回家中,那么小明的爸爸离家的距离S(单位:米)与离家的时间t(单位:分)之间的函数关系图象大致是( )A、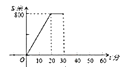 B、
B、 C、
C、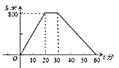 D、
D、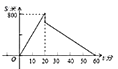 8. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1m),却踩伤了花草
8. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1m),却踩伤了花草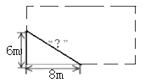 A、4 B、6 C、7 D、89. 两个一次函数 与 ,它们在同一直角坐标系中的图象可能是( )A、
A、4 B、6 C、7 D、89. 两个一次函数 与 ,它们在同一直角坐标系中的图象可能是( )A、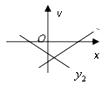 B、
B、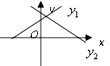 C、
C、 D、
D、 10. 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上, 则∠ADO的度数是( )
10. 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上, 则∠ADO的度数是( )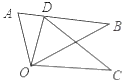 A、30° B、55° C、65° D、75°11. 某工厂共有60名员工,他们的月工资方差是s2 , 现在给每个员工的月工资增加300元,那么他们的新工资的方差( )A、变为s2+300 B、不变 C、变大了 D、变小了12. 如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PMN的面积;③△PAB的周长;④∠APB的大小;⑤直线MN,AB之间的距离.其中会随点P的移动而不改变的是( )
A、30° B、55° C、65° D、75°11. 某工厂共有60名员工,他们的月工资方差是s2 , 现在给每个员工的月工资增加300元,那么他们的新工资的方差( )A、变为s2+300 B、不变 C、变大了 D、变小了12. 如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PMN的面积;③△PAB的周长;④∠APB的大小;⑤直线MN,AB之间的距离.其中会随点P的移动而不改变的是( )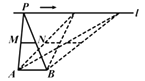 A、①②③ B、①②⑤ C、②③④ D、②④⑤
A、①②③ B、①②⑤ C、②③④ D、②④⑤二、填空题
-
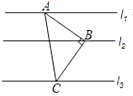
13. 若点A(-3,n)在x轴上,则点B(n-1,n+1)关于原点对称的点的坐标为 .14. 一次函数y=﹣2x+ 的图象与y轴的交点坐标是 .15. 如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3 . 若l1与l2的距离为4,l2与l3的距离为6,则Rt△ABC的面积为 .
 16. 如图在Rt△ABC中,∠ACB=90°,CD垂直AB于点D,∠ACD=4∠BCD,E是斜边AB的中点,∠ECD= .
16. 如图在Rt△ABC中,∠ACB=90°,CD垂直AB于点D,∠ACD=4∠BCD,E是斜边AB的中点,∠ECD= .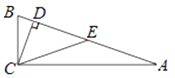 17. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为 .
17. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为 .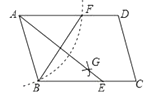 18. 已知点A(1,5),B(3,1),点M在x轴上,当AM+BM最小时,点M的坐标为 .
18. 已知点A(1,5),B(3,1),点M在x轴上,当AM+BM最小时,点M的坐标为 .
三、解答题
-
19. 一次函数y=kx-5的图象经过点(-3,-2),则:(1)、求这个函数表达式;(2)、判断(-5,-3)是否在此函数的图象上;20.
已知:四边形ABCD中,AC⊥BC,AB=17,BC=8,CD=12,DA=9;
 (1)、求AC的长(2)、求四边形ABCD的面积21. 如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)、求AC的长(2)、求四边形ABCD的面积21. 如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.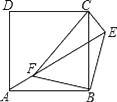 (1)、求证:△ABF≌△CBE;(2)、判断△CEF的形状,并说明理由.
(1)、求证:△ABF≌△CBE;(2)、判断△CEF的形状,并说明理由.
22.如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
 (1)、求证:△BCD≌△FCE;(2)、若EF∥CD,求∠BDC的度数.23.
(1)、求证:△BCD≌△FCE;(2)、若EF∥CD,求∠BDC的度数.23.今年我市九年级学业水平考试结束后,乐乐查到了自己的成绩,如下图(单位:分):
 (1)、请写出上图中所列数据的中位数和众数;(2)、我市规定:高中阶段招生录取成绩以分数形式呈现,按学业考试所有考试科目得分折合计算,其中语文、数学、英语按学业考试成绩100%计入,理科综合按150分(物理按65%、化学按45%、生物按40%)、文科综合按150分(思想品德按60%、历史按55%、地理按35%)、体育按50%、信息技术和理化实验技能操作各按20%计入。请你计算乐乐折合后的实际得分是多少?24. 如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)、请写出上图中所列数据的中位数和众数;(2)、我市规定:高中阶段招生录取成绩以分数形式呈现,按学业考试所有考试科目得分折合计算,其中语文、数学、英语按学业考试成绩100%计入,理科综合按150分(物理按65%、化学按45%、生物按40%)、文科综合按150分(思想品德按60%、历史按55%、地理按35%)、体育按50%、信息技术和理化实验技能操作各按20%计入。请你计算乐乐折合后的实际得分是多少?24. 如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.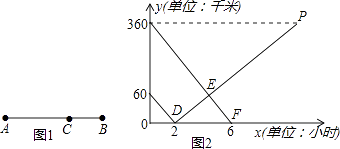 (1)、填空:A,B两地相距千米;(2)、求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;(3)、客、货两车何时相遇?25. 在矩形ABCD中,∠DAB的平分线交BC于点E,交DC的延长线于点F,连接BD.
(1)、填空:A,B两地相距千米;(2)、求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;(3)、客、货两车何时相遇?25. 在矩形ABCD中,∠DAB的平分线交BC于点E,交DC的延长线于点F,连接BD.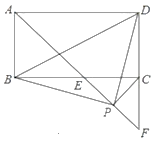 (1)、计算∠AEC的度数;(2)、求证:BE=DC;(3)、点P是线段EF上一动点(不与点E,F重合),在点P运动过程中,能否使△BDP成为等腰直角三角形?若能,写出点P满足的条件并证明;若不能,请说明理由.
(1)、计算∠AEC的度数;(2)、求证:BE=DC;(3)、点P是线段EF上一动点(不与点E,F重合),在点P运动过程中,能否使△BDP成为等腰直角三角形?若能,写出点P满足的条件并证明;若不能,请说明理由.