2017年山东省济南市市中区中考数学三模试卷
试卷日期:2017-07-25 考试类型:中考模拟
一、选择题
-
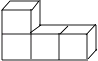
1. ﹣2的相反数是( )A、﹣ B、 C、﹣2 D、22. 如图是由4个大小相同的正方体组合而成的几何体,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为( )A、3.386×108 B、0.3386×109 C、33.86×107 D、3.386×1094. 如图,直线l1∥l2 , CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
3. 据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为( )A、3.386×108 B、0.3386×109 C、33.86×107 D、3.386×1094. 如图,直线l1∥l2 , CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )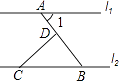 A、50° B、45° C、40° D、30°5. 下列运算正确的是( )A、 ﹣ = B、(﹣3)2=6 C、3a4﹣2a2=a2 D、(﹣a3)2=a56. 下列是轴对称图形的是( )A、
A、50° B、45° C、40° D、30°5. 下列运算正确的是( )A、 ﹣ = B、(﹣3)2=6 C、3a4﹣2a2=a2 D、(﹣a3)2=a56. 下列是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 图中的两个三角形是位似图形,它们的位似中心是( )
7. 图中的两个三角形是位似图形,它们的位似中心是( )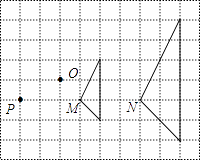 A、点P B、点O C、点M D、点N8. 化简分式 ÷ ,正确的结果是( )A、 B、 C、a﹣1 D、a9. 如图,在平面直角坐标系xOy中,点A为(0,3),点B为(2,1),点C为(2,﹣3).则经画图操作可知:△ABC的外心坐标应是( )
A、点P B、点O C、点M D、点N8. 化简分式 ÷ ,正确的结果是( )A、 B、 C、a﹣1 D、a9. 如图,在平面直角坐标系xOy中,点A为(0,3),点B为(2,1),点C为(2,﹣3).则经画图操作可知:△ABC的外心坐标应是( )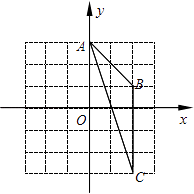 A、(0,0) B、(1,0) C、(﹣2,﹣1) D、(2,0)10. 三角形两边长分别为5和8,第三边是方程x2﹣6x+8=0的解,则此三角形的周长是( )A、15 B、17 C、15或17 D、不能确定11. 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )
A、(0,0) B、(1,0) C、(﹣2,﹣1) D、(2,0)10. 三角形两边长分别为5和8,第三边是方程x2﹣6x+8=0的解,则此三角形的周长是( )A、15 B、17 C、15或17 D、不能确定11. 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )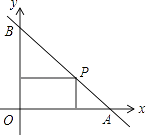 A、y=x+5 B、y=x+10 C、y=﹣x+5 D、y=﹣x+1012. 如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( )
A、y=x+5 B、y=x+10 C、y=﹣x+5 D、y=﹣x+1012. 如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( )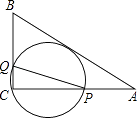 A、4.75 B、4.8 C、5 D、413. 矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
A、4.75 B、4.8 C、5 D、413. 矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )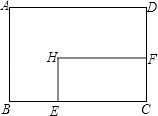 A、
A、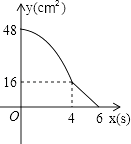 B、
B、 C、
C、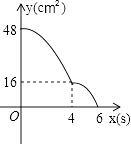 D、
D、 14. 设a,b是实数,定义@的一种运算如下:a@b=(a+b)2﹣(a﹣b)2 , 则下列结论:
14. 设a,b是实数,定义@的一种运算如下:a@b=(a+b)2﹣(a﹣b)2 , 则下列结论:①若a@b=0,则a=0或b=0
②a@(b+c)=a@b+a@c
③不存在实数a,b,满足a@b=a2+5b2
④设a,b是矩形的长和宽,若矩形的周长固定,则当a=b时,a@b最大.
其中正确的是( )
A、②③④ B、①③④ C、①②④ D、①②③二、填空题
-
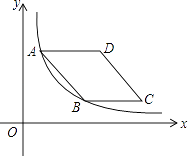
15. 分解因式:a3﹣a= .16. 计算: ﹣(2015﹣π)0﹣4cos45°= .17. 有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的中位数是 .18. 不等式 的解集是 .19. 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y= 的图象经过A,B两点,则菱形ABCD的面积为 .
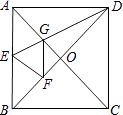
 20. 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:
20. 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4
其中正确有 .
三、解答题
-
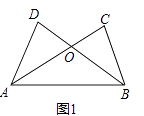
21. 综合题。(1)、先化简,再求值:a(a﹣2b)+(a+b)2 , 其中a=﹣1,b= .(2)、解方程: = .22. 综合题。(1)、如图1,已知AD=BC,AC=BD.求证:△ADB≌△BCA.
 (2)、如图2,已知AB是⊙O的一条直径,延长AB至点C,使AC=3BC,CD与⊙O相切于点D,若CD= ,求⊙O的半径.
(2)、如图2,已知AB是⊙O的一条直径,延长AB至点C,使AC=3BC,CD与⊙O相切于点D,若CD= ,求⊙O的半径.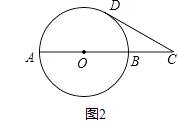 23. 有一个运输队承包了一家公司运送货物的业务,第一次运送18吨,派了一辆大卡车和5辆小卡车;第二次运送38吨,派了两辆大卡车和11辆小卡车,并且两次派的车都刚好装满.两种车型的载重量各是多少?24. 小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
23. 有一个运输队承包了一家公司运送货物的业务,第一次运送18吨,派了一辆大卡车和5辆小卡车;第二次运送38吨,派了两辆大卡车和11辆小卡车,并且两次派的车都刚好装满.两种车型的载重量各是多少?24. 小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).月均用水量(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
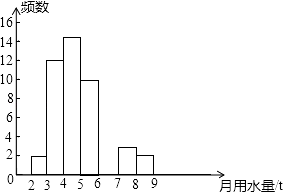 (1)、请根据题中已有的信息补全频数分布表和频数分布直方图;(2)、如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?(3)、从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.25. 如图,在平面直角坐标系中,直线AB与x轴交于点B、与y轴交于点A,与反比例函数y= 的图象在第二象限交于C,CE⊥x轴,垂足为点E,tan∠ABO= ,OB=4,OE=2.
(1)、请根据题中已有的信息补全频数分布表和频数分布直方图;(2)、如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?(3)、从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.25. 如图,在平面直角坐标系中,直线AB与x轴交于点B、与y轴交于点A,与反比例函数y= 的图象在第二象限交于C,CE⊥x轴,垂足为点E,tan∠ABO= ,OB=4,OE=2.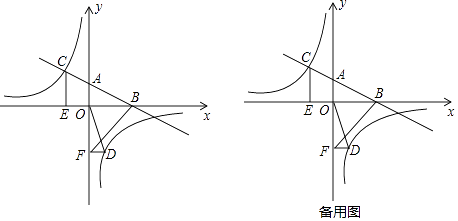 (1)、求反比例函数的解析式;(2)、若点D是反比例函数图象在第四象限内的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.(3)、若动点D在反比例函数图象的第四象限上运动,当线段DC与线段DB之差达到最大时,求点D的坐标.26. 在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)、求反比例函数的解析式;(2)、若点D是反比例函数图象在第四象限内的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.(3)、若动点D在反比例函数图象的第四象限上运动,当线段DC与线段DB之差达到最大时,求点D的坐标.26. 在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE. (1)、如图①,当∠ABC=45°时,求证:AD=DE;(2)、如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;(3)、当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)27. 如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.
(1)、如图①,当∠ABC=45°时,求证:AD=DE;(2)、如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;(3)、当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)27. 如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.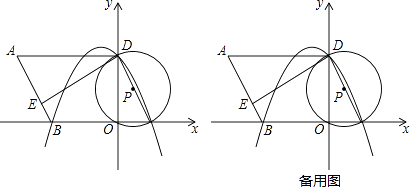 (1)、求抛物线的解析式;(2)、说明ED是⊙P的切线,若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线上吗?请说明理由;(3)、若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、说明ED是⊙P的切线,若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线上吗?请说明理由;(3)、若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.