山东省东营市四校连赛(五四制)2016-2017学年七年级下学期期末考试数学试题
试卷日期:2017-08-02 考试类型:期末考试
一、选择题
-
1. 下面4个图案,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、a3+a2=2a5 B、2a(1﹣a)=2a﹣2a2 C、(﹣ab2)3=a3b6 D、(a+b)2=a2+b23. 不等式-3x+2>-4的解集在数轴上表示正确的是( )A、
2. 下列运算正确的是( )A、a3+a2=2a5 B、2a(1﹣a)=2a﹣2a2 C、(﹣ab2)3=a3b6 D、(a+b)2=a2+b23. 不等式-3x+2>-4的解集在数轴上表示正确的是( )A、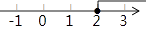 B、
B、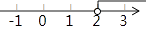 C、
C、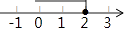 D、
D、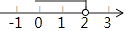 4. 化简: =( )A、0 B、1 C、x D、5. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
4. 化简: =( )A、0 B、1 C、x D、5. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )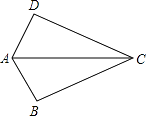 A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°6.
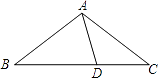
A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°6.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
 A、40° B、36° C、30° D、25°7. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A、40° B、36° C、30° D、25°7. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )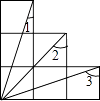 A、90° B、135° C、150° D、180°8. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于D,则DE的长为( )
A、90° B、135° C、150° D、180°8. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于D,则DE的长为( )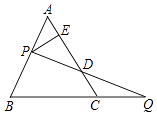 A、 B、 C、 D、9. 为了了解某市初一年级11000名学生的视力情况,抽查了1000名学生的视力进行统计分析.下面四种说法正确的是( )A、11000名学生是总体 B、每名学生是总体的一个个体 C、样本容量是11000 D、1000名学生的视力是总体的一个样本10. 下列命题中,正确的是( )A、三角形的一个外角大于任何一个内角 B、三角形的一条中线将三角形分成两个面积相等的三角形 C、两边和其中一边的对角分别相等的两个三角形全等 D、三角形的三条高都在三角形内部
A、 B、 C、 D、9. 为了了解某市初一年级11000名学生的视力情况,抽查了1000名学生的视力进行统计分析.下面四种说法正确的是( )A、11000名学生是总体 B、每名学生是总体的一个个体 C、样本容量是11000 D、1000名学生的视力是总体的一个样本10. 下列命题中,正确的是( )A、三角形的一个外角大于任何一个内角 B、三角形的一条中线将三角形分成两个面积相等的三角形 C、两边和其中一边的对角分别相等的两个三角形全等 D、三角形的三条高都在三角形内部二、填空题
-
11. 分解因式:a2b-b3= .12. 若一个正n边形的每个内角为156°,则这个正n边形的边数是13.
在图中涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形可以有个
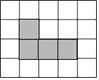 14. 如果二次三项式x2-mx+9是一个完全平方式,则实数m的值是 .15. 关于x的分式方程 =﹣2解为正数,则m的取值范围是 .16. 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是 .
14. 如果二次三项式x2-mx+9是一个完全平方式,则实数m的值是 .15. 关于x的分式方程 =﹣2解为正数,则m的取值范围是 .16. 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是 .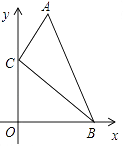 17.
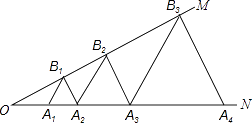
17.如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1 , 第2个等边三角形的边长记为a2 , 以此类推.若OA1=1,则a2017=.
三、解答题
-
18.
如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).
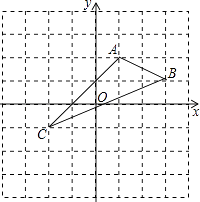 (1)、在图中作出△ABC关于y轴对称的△A1B1C1 .(2)、写出A1 , B1 , C1的坐标(直接写出答案),A1;B1;C1 .(3)、△ A1B1C1的面积为 .19.
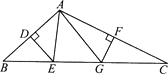
(1)、在图中作出△ABC关于y轴对称的△A1B1C1 .(2)、写出A1 , B1 , C1的坐标(直接写出答案),A1;B1;C1 .(3)、△ A1B1C1的面积为 .19.如图,△ABC中,BC=10,AB的垂直平分线分别交AB、BC于点D、E,A C的垂直平分线分别交A C、BC于点F、G.求△AEG的周长.
 20. 计算:
20. 计算:
(1)、(-2xy2)2÷ xy
(2)、(x+2)2+2(x+2)(x-4)-(x+3)(x-3)21. 先化简,再求值:(a+ )÷(1+ ).其中a是不等式组 的整数解.22. 在某市开展的“读中华经典,做书香少年”读书月活动中,围绕学生日人均阅读时间这一问题,对初二学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请你根据图中提供的信息解答下列问题: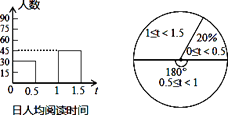 (1)、本次抽样调查的样本容量是多少?(2)、请将条形统计图补充完整.
(1)、本次抽样调查的样本容量是多少?(2)、请将条形统计图补充完整.
(3)、在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角度数.(4)、根据本次抽样调查,试估计该市12000名初二学生中日人均阅读时间在0.5~1.5小时的是多少人.
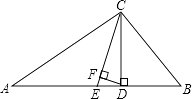
23.如图,△ABC中,∠A=40°,∠B=76°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.
 24. 如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,
24. 如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,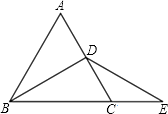 (1)、求证:DB=DE.(2)、在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
(1)、求证:DB=DE.(2)、在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
25. 东营市某学校2015年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.(1)、求购买一个甲种足球、一个乙种足球各需多少元;(2)、2016年为响应习总书记“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%.如果此次购买甲、乙两种足球的总费用不超过2900元,那么这所学校最多可购买多少个乙种足球?26.在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD。
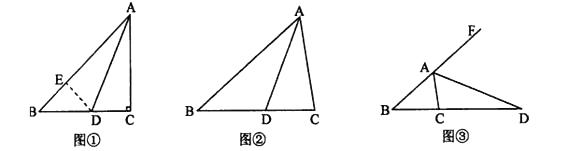 (1)、如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明;(2)、如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明。
(1)、如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明;(2)、如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明。