相关试卷

1、如图，已知斜坡AB，且 $B C ⊥ A C$ ，则斜坡AB的坡比指的是（）

A、AB：BC B、AB：AC C、AC：BC D、BC：AC

查看解析
2、化简 $\sqrt{\frac{1}{4}}$ ，结果为（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、-2 D、2

查看解析
3、如图1，△ABC内接于⊙O，AB=AC，过点C作CD//AB，交⊙O于D，过D作DE⊥AB于点E，交BC于点M，连接AD.

(1)、求证：AD=BC；

(2)、AD²=2AE·AB.

(3)、如图2，若M是BC中点，求 $\frac{A B}{B C}$ 的值.

查看解析
4、抛物线y=ax²+bx+c经过A（0，4）和B（2，0）两点.

(1)、求c的值及a，b满足的关系式.

(2)、抛物线同时经过两个不同的点M（k，m）和N（-2-k，m），求b的值.

(3)、若抛物线在A和B两点间y随x的增大而减少，求a的取值范围．

查看解析
5、星期日上午9：00，小明从家里出发步行前往离家2.4km的金华书城参加读书会活动，他以75m/min的速度步行了12min后发现忘带入场券，于是他停下来。打电话给家里的爸爸寻求帮助，9：15爸爸骑着自行车从家里出发，沿着同一路线以375m/min的速度行进，同一时刻小明继续按原速步行赶往目的地。爸爸追上小明后载上他以相同的车速前往书城（停车载人时间忽略不计），到达书城后爸爸原速返回家，爸爸和小明离家的路程s（m）与小明所用时间（（min）的函数关系如图所示.

(1)、求爸爸在到达金华书城前，他离开家的路程s关于：的函数表达式及a的值：

(2)、爸爸出发后多长时间追上小明？此时距离金华书城还有多远?

查看解析
6、为了解全校学生对篮球、足球、乒乓球、羽毛球四项球类运动的喜爱情况，在全校随机抽取了m名学生进行问卷调查，每名学生只选择一项球类运动填写问卷，将调查结果绘制成如图统计图，请你根据图中所提供的信息解答下列问题

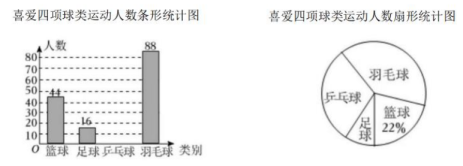(1)、求m= ，并补全条形统计图

(2)、若该校共有1200名学生，请估计喜欢乒乓球运动的学生有多少名？

(3)、学校羽毛球队计划从甲、乙、丙、丁四名同学中挑选两名同学加入球队.请用画树状图或列表的方法计算恰好选中甲、乙两名同学的概率，

查看解析
7、如图，在 $8 \times 6$ 的方格中， $△ A B C$ 是格点三角形（顶点均在格点上），请按要求画图。

(1)、在图1中，作格点 $△ A E F$ ，使得 $△ A E F$ 与 $△ A B C$ 相似，且相似比为2：1；

(2)、在图2中画出 $△ A B C$ 绕着格点0顺时针旋转 $9 0^{°}$ 得到的 $△ M N F$

查看解析
8、先化简，再求值： $\frac{x}{x^{2} - 1} \div (\frac{x}{1 - x} + 1)$ ，其中 $x = 3$ ．

查看解析
9、计算： $(- 1)^{2025} + | \sqrt{3} - 2 | - \sqrt{2} s i n 4 5^{°} + \sqrt[3]{27}$

查看解析
10、当m≤x≤m+1，函数y=x²-2x-1的最小值为2，则m的值为.

查看解析
11、如图，AB为⊙O的切线，点A为切点，OB交⊙0于点C，点D在⊙O上，连接AD，CD，若∠ADC=25°，则∠ABO的度数为度

查看解析
12、如图，在∠ABC中，AB=4，BC=7，∠B=60°，将∠ABC绕点A顺时针旋转到∠ADE，D刚好在BC上，则CD=.

查看解析
13、一元二次方程（x-1）=2x（x-1）的解是.

查看解析
14、因式分解x²y-y=.

查看解析
15、如图，在菱形ABCD中， $∠ C = 6 0^{°}, A D = 2$ ，连接BD，0是BD的中点， $E$ 是DA延长线上的一点，连接OE，作 $∠ E O F = 12 0^{°}$ ，交AB的延长线于点 $F$ ，记 $B F = x, A E = y$ ，当x，y的值发生变化时，下列代数式的值不变的是（）

A、 $x + y$ B、 $x - y$ C、xy D、 $\frac{x}{y}$

查看解析
16、如图，将两个全等的边长为6的正六边形一边重合放置在一起，中心分别为 $O_{1} O_{2}$ ，连接 $O_{1} O_{2}$ 则 $O_{1} O_{2}$ 的长为（）

A、 $6 \sqrt{3}$ B、 $6 \sqrt{2}$ C、 $4 \sqrt{3}$ D、 $4 \sqrt{2}$

查看解析
17、在数轴上表示不等式 $x - 2 ⩽ 0$ 的解集，正确的是（）

A、 B、 C、 D、

查看解析
18、某九年一贯制学校由于学生较多，学校食堂采取错时用餐，初中部每个同学必须在30分钟用好午餐.为了给食堂管理提出合理的建议，小明同学调查了某日11：30下课后15分钟内进入食堂累计人数》（人）与经过的时间x分钟（x为自然数）之间的变化情况，部分数据如下：
经过的时间x/分钟
0
1
2
3
4
5
…
10
累计人数y（人）
0
95
180
255
320
375
…
500
当x>10时y与x之间的函数关系式y=10x+400，（10<x≤15）.
已知每位同学需排队取餐，食堂开放5个窗口，每个窗口每分钟4个同学取好餐。

(1)、根据上述数据，请利用已学知识，求出当x≤10时，y与x之间的函数关系式.

(2)、排队人数最多时有多少人？

(3)、若开始取餐x分钟后增设m个窗口（受场地限制，窗口总数不能超过10个），以便在11点40分时（第10分钟）正好完成前300位同学的取餐，求x，m的值.

查看解析
19、如图，7×7的的网格中，A，B，C均在格点上，请用无刻度的直尺作图（保留作图痕迹，不写作法）

(1)、在图1中找一格点D，使得△ACD为等腰三角形（不可以增加网格，找到一个即可）；
图1

(2)、在图2中作出∠BAC的角平分线.
图2

查看解析
20、为了增强学生的安全意识，某校开展了主题为“科学防护·珍爱生命”的安全知识竞赛，现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：A.80≤x<85，B.85≤x<90，C.90
≤x<95，D.95≤x≤100），下面给出了部分信息：
七年级10名学生的竞赛成绩是：99，80，99，86，99，96，90，100，89，82.
八年级10名学生的竞赛成绩在C组中的数据是：94，90，94.
七、八年级抽取的学生竞赛成绩统计表
年级
七年级
八年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4
根据以上信息，解答下列问题：

(1)、直接写出上述图表中 a， b，c的值；

(2)、根据以上数据，你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好？请说明理由（写出一条理由即可），

查看解析

上一页 28 29 30 31 32 下一页跳转

经过的时间x/分钟	0	1	2	3	4	5	…	10
累计人数y（人）	0	95	180	255	320	375	…	500

年级	七年级	八年级
平均数	92	92
中位数	93	b
众数	c	100
方差	52	50.4