山东省德州地区2016-2017学年度下学期期末测试七年级数学试题

试卷日期：2017-07-28 考试类型：期末考试

前去【出卷网】下载

一、选择题

1. 为了了解某校七年级400名学生的体重情况，从中抽取50名学生进行统计分析，在这个问题中，总体是指（）。

A、400 B、被抽取的50名学生 C、400名学生的体重 D、被抽取的50名学生的体重

查看试题解析
2. 下列六种说法正确的个数是（）
①无限小数都是无理数；
②正数、负数统称实数数；
③无理数的相反数还是无理数；
④无理数与无理数的和一定还是无理数；
⑤无理数与有理数的和一定是无理数；
⑥无理数与有理数的积一定仍是无理数．

A、1 B、2 C、3 D、4

查看试题解析
3. 若点P（a-2，a）在第二象限，则a的取值范围是（）

A、0＜a＜2 B、-2＜a＜0 C、a＞2 D、a＜0

查看试题解析
4. 在平面直角坐标系中，点（-3， $- x^{2} - 1$ ）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 如图，下列条件能判断两直线AB，CD平行的是（）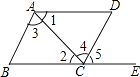

A、∠1=∠2 B、∠3=∠4 C、∠1=∠5 D、∠3=∠5

查看试题解析
6. 若a＞b，则下列式子正确的是（）

A、﹣5a＞﹣5b B、a﹣3＞b﹣3 C、4﹣a＞4﹣b D、 $\frac{1}{2}$ a $<$ $\frac{1}{2}$ b

查看试题解析
7. 已知x,y满足方程 ${\begin{matrix} 2 x + y = 4 \\ x + 2 y = 5 \end{matrix}$ ，则x-y等于（）

A、9 B、3 C、1 D、-1

查看试题解析
8. 如图：AB∥CD，直线MN与AB交于E，过点E作直线HE⊥MN，∠1=130°，则∠2等于（）

A、50° B、40° C、30° D、60°

查看试题解析
9. 已知不等式2x－a≤0的正整数解恰好是1,2,3,4,5,那么a的取值范围是（）

A、a＞10 B、10≤a≤12 C、10＜a≤12 D、10≤a＜12

查看试题解析
10. 甲、乙两种商品原来的单价和为100元，因市场变化，甲商品降价10%，乙商品提价40%，调价后两种商品的单价和比原来的单价和提高了20%、若设甲、乙两种商品原来的单价分别为x元、y元，则下列方程组正确的是（）

A、 ${\begin{matrix} x + y = 100 \\ (x + 10 ％) x + (1 - 40 ％) y = 100 (1 + 20 ％） \end{matrix}$ B、 ${\begin{matrix} x + y = 100 \\ (1 - 10 ％) x + (1 + 40 ％) y = 100 (1 + 20 ％） \end{matrix}$ C、 ${\begin{matrix} x + y = 100 \\ (x - 10 ％) x + (1 + 40 ％) y = 100 \times 20 ％ \end{matrix}$ D、 ${\begin{matrix} x + y = 100 \\ (x + 10 ％) x + (1 - 40 ％) y = 100 \times 20 ％ \end{matrix}$

查看试题解析
11. 下列选项中正确的是（）

A、27的立方根是±3 B、 $\sqrt{16}$ 的平方根是±4 C、9的算术平方根是3 D、立方根等于平方根的数是1

查看试题解析
12.
如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2015次运动后，动点P的坐标是（）

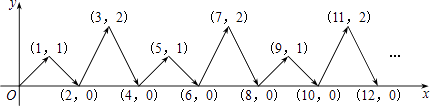A、（2015，0） B、（2015，1） C、（2015，2） D、（2016，0）

查看试题解析

二、填空题

13. 统计得到一组数据，最大值是136，最小值是52，取组距为10，可以分成组。

查看试题解析
14.
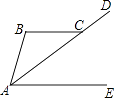
如图，已知直线AE∥BC，AD平分∠BAE，交BC于点C，∠BCD=140°，则∠B的度数为

查看试题解析
15. 若关于x,y的二元一次方程组 ${\begin{matrix} x - y = 4 k ① \\ x + y = 2 k ② \end{matrix}$ 的解也是二元一次方程x-3y=6的解，则k等于

查看试题解析
16. 某大型超市从生产基地购进一批水果,运输及销售中估计有10%的苹果正常损耗,苹果的进价是每千克1.8元,商家要避免亏本,需把售价至少定为元

查看试题解析
17. 在平面直角坐标系中，按照一定规律写出了如下各点坐标：点A1（2，2），A2（3，5），A3（4，10），A4（5，17），…请你仔细观察，按照此规律点A10的坐标应为.

查看试题解析

三、解答题

18. 解方程组 ${\begin{matrix} 5 x - y = 4 \\ \frac{x}{2} + 1 = \frac{y}{3} \end{matrix}$

查看试题解析
19. 计算： $2 \sqrt{2} + \sqrt{9} + \sqrt[3]{- 8} + | \sqrt{2} - 2 |$

查看试题解析
20. 解不等式组： $\{\begin{matrix} \frac{x + 2}{3} - 1 > x \\ 2 (1 - x) \leq 5 \end{matrix}$ ，并把其解集在数轴上表示出来。

查看试题解析
21.
完成下面的证明。
已知：如图，BE∥CD，∠A＝∠1，
求证：∠C＝∠E。

证明：∵BE∥CD （已知）
∴∠2=∠C （                          ）
又 ∵∠A=∠1 （已知）
∴ AC∥DE （                           ）
∴ ∠2＝∠E（                           ）
∴∠C=∠E （                    ）

查看试题解析