2017年山东省临沂市蒙阴县中考数学二模试卷
试卷日期:2017-07-25 考试类型:中考模拟
一、选择题
-
1. 的相反数是( )A、2 B、﹣2 C、 D、﹣2. 下列计算正确的是( )A、x+x2=x3 B、x2•x3=x6 C、(x3)2=x6 D、x9÷x3=x33. 如图,能判定EB∥AC的条件是( )
 A、∠A=∠ABE B、∠A=∠EBD C、∠C=∠ABC D、∠C=∠ABE4. 如图是由4个相同的小正方形搭成的一个几何体,则它的俯视图是( )
A、∠A=∠ABE B、∠A=∠EBD C、∠C=∠ABC D、∠C=∠ABE4. 如图是由4个相同的小正方形搭成的一个几何体,则它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 某班第一组12名同学在“爱心捐款”活动中,捐款情况统计如下表,则捐款数组成的一组数据中,中位数与众数分别是( )
5. 某班第一组12名同学在“爱心捐款”活动中,捐款情况统计如下表,则捐款数组成的一组数据中,中位数与众数分别是( )捐款(元)
10
15
20
50
人数
1
5
4
2
A、15,15 B、17.5,15 C、20,20 D、15,206. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠17. 化简 结果正确的是( )A、ab B、﹣ab C、a2﹣b2 D、b2﹣a28. 如图,⊙O是△ABC的外接圆,连接OA、OB,∠OBA=50°,则∠C的度数为( )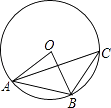 A、30° B、40° C、50° D、80°9. 如果点P(2x+6,x﹣4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为( )
A、30° B、40° C、50° D、80°9. 如果点P(2x+6,x﹣4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为( )
A、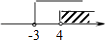 B、
B、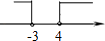 C、
C、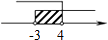 D、
D、 10. 四张质地、大小、背面完全相同的卡片上,正面分别画有圆、矩形、等边三角形、等腰梯形四个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为( )A、 B、 C、 D、111. 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )
10. 四张质地、大小、背面完全相同的卡片上,正面分别画有圆、矩形、等边三角形、等腰梯形四个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为( )A、 B、 C、 D、111. 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( ) A、13 B、14 C、15 D、1612. 如图,双曲线y= (k>0)与⊙O在第一象限内交于P、Q两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为( )
A、13 B、14 C、15 D、1612. 如图,双曲线y= (k>0)与⊙O在第一象限内交于P、Q两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为( ) A、1 B、2 C、3 D、413. 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A、1 B、2 C、3 D、413. 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )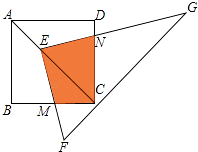 A、 a2 B、 a2 C、 a2 D、 a214. 如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y= +bx+c的顶点,则抛物线y= +bx+c与直线y=1交点的个数是( )
A、 a2 B、 a2 C、 a2 D、 a214. 如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y= +bx+c的顶点,则抛物线y= +bx+c与直线y=1交点的个数是( )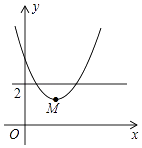 A、0个或1个 B、0个或2个 C、1个或2个 D、0个、1个或2个
A、0个或1个 B、0个或2个 C、1个或2个 D、0个、1个或2个二、填空题
-
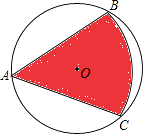
15. 分解因式:2x2﹣8= .16. 方程 ﹣ =0的解为x= .17. 有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC,用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r= .
 18. 如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH= .
18. 如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH= .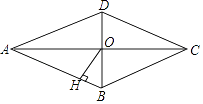 19. 如果一个数的平方等于﹣1,记作i2=﹣1,这个数叫做虚数单位.形如a+bi(a,b为有理数)的数叫复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
19. 如果一个数的平方等于﹣1,记作i2=﹣1,这个数叫做虚数单位.形如a+bi(a,b为有理数)的数叫复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.如:(2+i)+(3﹣5i)=(2+3)+(1﹣5)i=5﹣4i,
(5+i)×(3﹣4i)=5×3+5×(﹣4i)+i×3+i×(﹣4i)=15﹣20i+3i﹣4×i2=15﹣17i﹣4×(﹣1)=19﹣17i.
请根据以上内容的理解,利用以前学习的有关知识将(1+i)(1﹣i)化简结果为为 .
三、解答题
-
20. 计算:( )﹣1﹣(﹣2014)0﹣2cos45°+ .21. 某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:
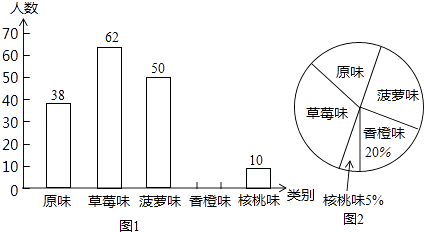 (1)、本次被调查的学生有名;(2)、补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;(3)、该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?22. 已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)、本次被调查的学生有名;(2)、补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;(3)、该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?22. 已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.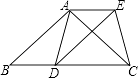 (1)、求证:AD=CE;(2)、当点D在什么位置时,四边形ADCE是矩形,请说明理由.23. 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2 .
(1)、求证:AD=CE;(2)、当点D在什么位置时,四边形ADCE是矩形,请说明理由.23. 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2 . (1)、求AC的长度;(2)、求图中阴影部分的面积.(计算结果保留根号)24. 我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
(1)、求AC的长度;(2)、求图中阴影部分的面积.(计算结果保留根号)24. 我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:销售单价x(元/件)
…
30
40
50
60
…
每天销售量y(件)
…
500
400
300
200
…
(1)、把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式; (2)、当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)(3)、当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?25. 问题探究:
(2)、当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)(3)、当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?25. 问题探究:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
 (1)、证明:AD=BE;(2)、求∠AEB的度数.(3)、如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.
(1)、证明:AD=BE;(2)、求∠AEB的度数.(3)、如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.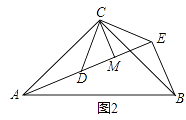 26. 如图,点A的坐标为(﹣8,0),点P的坐标为 ,直线y= x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
26. 如图,点A的坐标为(﹣8,0),点P的坐标为 ,直线y= x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.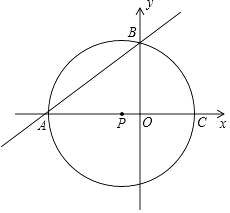 (1)、判断点B是否在⊙P上?说明理由.(2)、求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.(3)、⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、判断点B是否在⊙P上?说明理由.(2)、求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.(3)、⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.