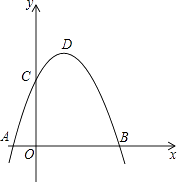山东省青岛市2016-2017学年中考四模数学考试试卷
试卷日期:2017-08-23 考试类型:中考模拟
一、选择题
-
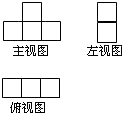
1. 下列式子:x2+1, +4, , ,﹣5x,0中,整式的个数是( )A、6 B、5 C、4 D、32. 一个物体由多个完全相同的小正方体组成,它的三视图如图所示,那么组成这个物体的小正方体的个数为( )
 A、2 B、3 C、4 D、53. 如图是一架婴儿车,其中AB∥CD,∠1=130°,∠3=40°,那么∠2是( )
A、2 B、3 C、4 D、53. 如图是一架婴儿车,其中AB∥CD,∠1=130°,∠3=40°,那么∠2是( )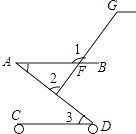 A、80° B、90° C、100° D、102°4. 下列说法中正确的是( )A、4的平方根是2 B、点(﹣3,﹣2)关于x轴的对称点是(﹣3,2) C、是无理数 D、无理数就是无限小数5. 下列说法正确的是( )A、为了了解全国中学生每天体育锻炼的时间,应采用普查的方式 B、若甲组数据的方差s =0.03,乙组数据的方差是s =0.2,则乙组数据比甲组数据稳定 C、广安市明天一定会下雨 D、一组数据4、5、6、5、2、8的众数是56. 下列所给的方程中没有实数根的是( )A、x2=3x B、5x2﹣4x﹣1=0 C、3x2﹣4x+1=0 D、4x2﹣5x+2=07. 如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m>kx﹣1的解集在数轴上表示正确的是( )
A、80° B、90° C、100° D、102°4. 下列说法中正确的是( )A、4的平方根是2 B、点(﹣3,﹣2)关于x轴的对称点是(﹣3,2) C、是无理数 D、无理数就是无限小数5. 下列说法正确的是( )A、为了了解全国中学生每天体育锻炼的时间,应采用普查的方式 B、若甲组数据的方差s =0.03,乙组数据的方差是s =0.2,则乙组数据比甲组数据稳定 C、广安市明天一定会下雨 D、一组数据4、5、6、5、2、8的众数是56. 下列所给的方程中没有实数根的是( )A、x2=3x B、5x2﹣4x﹣1=0 C、3x2﹣4x+1=0 D、4x2﹣5x+2=07. 如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m>kx﹣1的解集在数轴上表示正确的是( )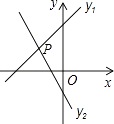 A、
A、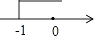 B、
B、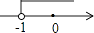 C、
C、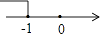 D、
D、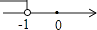 8. 如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CF相交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( )
8. 如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CF相交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( )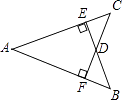 A、① B、② C、①② D、①②③9. 已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为( )
A、① B、② C、①② D、①②③9. 已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为( )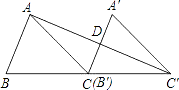 A、6 B、9 C、12 D、1810. 对于数对(a,b)、(c,d),定义:当且仅当a=c且b=d时,(a,b)=(c,d);并定义其运算如下:
A、6 B、9 C、12 D、1810. 对于数对(a,b)、(c,d),定义:当且仅当a=c且b=d时,(a,b)=(c,d);并定义其运算如下:(a,b)※(c,d)=(ac﹣bd,ad+bc),如(1,2)※(3,4)=(1×3﹣2×4,1×4+2×3)=(﹣5,10).若(x,y)※(1,﹣1)=(1,3),则xy的值是( )
A、﹣1 B、0 C、1 D、211. 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( ) A、 B、 C、 D、12. 已知抛物线y=a(x﹣3)2+ 过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:
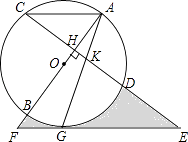
A、 B、 C、 D、12. 已知抛物线y=a(x﹣3)2+ 过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;
②点C在⊙D外;
③在抛物线上存在一点E,能使四边形ADEC为平行四边形;
④直线CM与⊙D相切.
正确的结论是( )
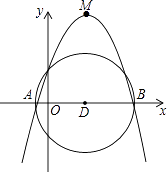 A、①③ B、①④ C、①③④ D、①②③④
A、①③ B、①④ C、①③④ D、①②③④二、填空题
-
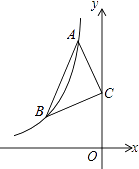
13. 化简: ﹣ = .14. 一个不透明的盒子里有4个除颜色外其他完全相同的小球,其中每个小球上分别标有1,﹣1,﹣2,﹣3四个不同的数字,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下数字后再放回盒子,那么两次摸出的小球上两个数字乘积是负数的概率为 .15. 小明参加了某电视台招聘记者的三项素质测试,成绩如下:采访写作70分,计算机操作60分,创意设计88分,如果采访写作、计算机操作和创意设计的成绩按4:1:3计算,则他的素质测试平均成绩为分.16. 如图,△ABC的顶点A,B都在反比例函数y=﹣ 的第二象限内的分支上,点C(0,3),且AC=BC,∠ACB=90°,则线段AB的长为 .
 17. 如图,点E(0,3),O(0,0),C(4,0)在⊙A上,BE是⊙A上的一条弦.则sin∠OBE= .
17. 如图,点E(0,3),O(0,0),C(4,0)在⊙A上,BE是⊙A上的一条弦.则sin∠OBE= .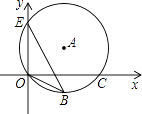 18. 用火柴棒按如图两种方式搭图形,若搭(x+1)个等边三角形与搭y个正六边形所用的火柴棒根数相同,则 的值为 .
18. 用火柴棒按如图两种方式搭图形,若搭(x+1)个等边三角形与搭y个正六边形所用的火柴棒根数相同,则 的值为 .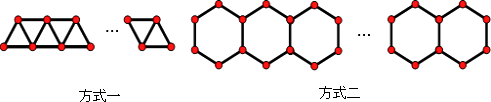
三、解答题
-
19. 先化简,再求值: ÷(x+1﹣ ),其中x=﹣8sin30°+2cos45°.20. 某种商品A的零售价为每件900元,为了适应市场竞争,商店按零售价的九折优惠后,再让利40元销售,仍可获利10%,
①这种商品A的进价为多少元?
②现有另一种商品B进价为600元,每件商品B也可获利10%.对商品A和B共进货100件,要使这100件商品共获纯利6670元,则需对商品A、B分别进货多少件?
21. 某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛,各参赛选手的成绩如下:九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级
最高分
平均分
中位数
众数
方差
九(1)班
100
94
b
93
12
九(2)班
99
a
95.5
93
8.4
(1)、直接写出表中a、b的值:a= , b=;(2)、若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.22. 如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH,其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°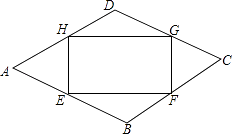 (1)、求S关于x的函数关系式,并直接写出自变量x的取值范围;(2)、若a=100,求S的最大值,并求出此时x的值.
(1)、求S关于x的函数关系式,并直接写出自变量x的取值范围;(2)、若a=100,求S的最大值,并求出此时x的值.