-
1、如图，在四边形ABCD中，AB=8cm， BC=6cm，∠B=90°，CD// AB，O是AC的中点，连结DO并延长，交AB于点E，连结CE.
(1)、求证：四边形AECD是平行四边形.(2)、若 CE 平分∠ACB，求 AD 的长. -
2、如图，在6×6的方格纸中，点A，B，P均在格点上，请按下列要求作格点三角形（顶点在格点上）.
(1)、作一个等腰三角形ABC，使得点P在△ABC的内部.(2)、在（1）的基础上，作△A'B'C，使得它和△ABC关于点P成中心对称. -
3、某校在课后服务中设置了体育相关的拓展课程，分别是A（篮球），B（足球），C（太极拳），D（健身操），为了解学生对上述课程的喜爱情况，随机抽取若干名学生进行最喜爱的体育拓展课程问卷调查（每人选择一门课程），并根据统计结果，绘制成如图所示的两幅不完整的统计图.
(1)、本次抽样调查，一共抽查了多少名学生.(2)、请估计全校900名学生中最喜爱太极拳的人数. -
4、解方程组
-
5、(1)、 计算：(2)、化简： （2a-b）2-4a（a-b）.
-
6、如图，在菱形ABCD中，对角线AC，BD相交于点O，E是边AB上一点，连结DE交AC于点F，将线段DE绕点D逆时针旋转至DE'，使得∠EDE'=∠ADC，若 ， 点E，O，E'在同一直线上，则△AEF与四边形BEFC 的面积比为.
-
7、 在直角坐标系中，含30°的Rt∠AOB如图放置，∠AOB=90°，∠B=30°，AB的中点C在х轴上，第一象限内点A在反比例函数y=图象上，则过第四象限内点B的反比例函数表达式是.
-
8、有A，B两种款式的帽子，C，D两种款式的围巾.小江任意选一顶帽子和一条围巾，恰好选中他所喜欢的A款帽子和C款围巾的概率是.
-
9、不等式组的解集为.
-
10、若扇形的圆心角为60°，半径为2，则它的弧长为.
-
11、 因式分解：m2-4m=.
-
12、 如图，在Rt△ABC中，∠ACB=90°，以其三边为边向外作正方形，线段 BC与 BC关于AB 对称，作 GJ⊥BC于点J，FK⊥GJ于点K，连结AC并延长交FK于点L，连结EH，CC' ， 若CC'=4，正方形CLKJ 的面积为 5，则EH 的长为（ ）
A、3 B、3 C、3 D、10 -
13、 已知AABC中，AC=BC=4，CD⊥AB于点D，E是AC的中点，CD交 BE于点O，若 CE=CO，则AB 的长是（ ）
A、5 B、2 C、6 D、10 -
14、 如图，AB为半圆O的直径，C为AB延长线上一点，CD切半圆于点D，AE⊥CD于点E，连结AD，若∠C=40°，则∠DAE 的度数是（ ）
A、20° B、25° C、28° D、30° -
15、 若分式的值是零，则x的值是（ ）A、-2 B、-1 C、1 D、2
-
16、某班五个小组在一次项目化学习中提出的问题个数分别是：5，3，6，4，7.则这五个小组提出问题个数的平均数是（ ）A、4 B、5 C、5.5 D、6
-
17、下列式子运算正确的是（ ）A、a6-a2=a4 B、（a6）2=a36 C、a6a2=a8 D、a6+a2=a3
-
18、5个大小一样的正方体按如图摆放，它的俯视图是（ ）
A、
B、
C、
D、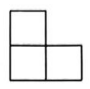
-
19、计算4+（-3）的结果是（ ）A、-1 B、1 C、-7 D、7
-
20、定义：已知x1 ， x2是关于x的一元二次方程a2+bx+c=0（a≠0）的两个实数根，若x12<0，且3<<4，则称这个方程为“限根方程”．比如：一元二次方程x2+13x+30=0的两根为x1=-10，x2=-3，因-10<-3<0，3<<4，所以一元二次方程x2+13x+30=0为“限根方程”，
请阅读以上材料，回答下列问题：
(1)、判断：一元二次方程x2+14x+33=0（填“是”或“不是”）“限根方程”.(2)、若关于x的一元二次方程x2+（k十9）x+k2+8=0是“限根方程”，且方程的两根x1、x2满足11x1+11x2+x1x2=-121，求k的值.(3)、若关于x的一元二次方程x2+（1-m）x-m=0是“限根方程”，求m的取值范围.