相关试卷

1、如图，在纸板中裁剪一款纸盒，减去阴影部分，再把剩下的纸片沿虚线折叠成一个有盖的长方体纸盒，设减去的正方形纸片边长为 $x cm$ ，长方形纸片的长为 $y cm$ ．

(1)、用含 $a$ 的代数式表示 $x$ ， $y$ ，则 $x =$ ____________ $cm$ ， $y =$ ____________ $cm$ ．

(2)、用含 $a$ 的代数式表示阴影部分的总面积．

(3)、若规定“当阴影部分面积超过总面积的 $15 %$ 时，属于无效设计”，则当 $a = 10 cm$ 时，请判断该设计是否有效，并说明理由．

查看解析
2、如图， $A E$ 与 $B D$ 相交于点F， $∠ B = ∠ C$ ， $∠ 1 = ∠ 2$ ．

(1)、试判断 $A B$ 与 $C E$ 的位置关系，并说明理由．

(2)、若 $A E$ 平分 $∠ B A C$ ， $∠ 2 = 72 °$ ，求 $∠ C$ 的度数．

查看解析
3、如图，在边长为1个单位的正方形网格中有一格点 $△ A B C$ ．

(1)、请在图1中将 $△ A B C$ 平移，使点A落在D，得到 $△ D B_{1} C_{1}$ ，画出 $△ D B_{1} C_{1}$ ．

(2)、请在图2中将 $△ A B C$ 平移，使点D、E都落在 $△ A_{2} B_{2} C_{2}$ 内部．

查看解析
4、（1）计算： $- 2^{2} + {(π - 3.14)}^{0} + 3^{- 1}$
（2）化简： ${(2 x - 1)}^{2} - x (x - 4)$

查看解析
5、图1是光伏发电场景，其示意图如图2， $O P$ 为吸热塔，在地平线上的点C，D处各安装定日镜（介绍见图3）．绕各中心点（A，B）旋转镜面，使过中心点的太阳光线经镜面反射后到达吸热器点O处．A、B处于同一水平高度，已知反射光线 $O A$ 与水平线 $M N$ 的夹角是 $25 °$ ，镜面 $A E$ 与立杆的夹角 $∠ E A C = 45 °$ ，则太阳光线 $A G$ 与水平面夹角 $∠ G A N =$ $°$ ；若反射光线 $O B$ 与水平线 $M N$ 的夹角是 $41 °$ 时，则 $∠ F B D =$ $°$ ．

查看解析
6、如图，将正方形 $A B C D$ 与正方形 $E F G H$ 叠在一起，且这两个正方形的边长之差为 $2 (A B > H G)$ ，两个正方形相交于点M、N，连结 $B M$ ， $B N$ ，若阴影部分的面积是9， $E M = 1$ ， $N G = 2$ ，则正方形 $E F G H$ 的边长为（）

A、 $\sqrt{13}$ B、4 C、4.2 D、4.5

查看解析
7、下列图形中， $∠ 1$ 与 $∠ 2$ 是同位角的是（）

A、 B、 C、 D、

查看解析
8、阅读与思考
请阅读下面材料，并完成相应的任务．
在学习完实数的相关运算之后，某数学兴趣小组提出了一个有趣的问题：两个数的积的算术平方根与这两个数的算术平方根的积存在什么关系？小聪和小明分别用自己的方法进行了验证：
小聪： $\sqrt{4 \times 25} = \sqrt{100} = 10$ ， $\sqrt{4 \times 25} = 2 \times 5 = 10$ ，
所以 $\sqrt{4 \times 25} = \sqrt{4} \times \sqrt{25}$ ．
小明： ${(\sqrt{4 \times 25})}^{2} = 4 \times 25 = 100$ ， ${(\sqrt{4 \times 25})}^{2} = {(2 \times 5)}^{2} = 100$ ．
这就说明 $\sqrt{4 \times 25}$ 和 $\sqrt{4} \times \sqrt{25}$ 都是 $4 \times 25$ 的算术平方根，而 $4 \times 25$ 的算术平方根只有一个，
所以 $\sqrt{4 \times 25} = \sqrt{4} \times \sqrt{25}$ ．
任务：

(1)、猜想：当 $a \geq 0$ ， $b \geq 0$ 时， $\sqrt{a b}$ 和 $\sqrt{a} \times \sqrt{b}$ 之间存在怎样的关系？并仿照小聪或小明的方法举出一个例子进行说明；

(2)、运用以上结论，计算：① $\sqrt{16 \times 36}$ ；② $\sqrt{49 \times 121}$ ；

(3)、解决实际问题：已知一个长方形的长为 $\sqrt{32}$ ，宽为 $\sqrt{8}$ ，求这个长方形的面积．

查看解析
9、某班将买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍．乒乓球拍每副定价50元，乒乓球每盒定价10元，经洽谈后，甲店每买一副球拍赠一盒乒乓球，乙店全部按定价的9折优惠．该班需球拍5副，乒乓球x盒（不小于5盒）问：

(1)、当需要40盒乒乓球时，通过计算，说明此时去哪家购买较为合算．

(2)、当购买乒乓球数为多少盒时，甲乙两家商店所需费用一样．

查看解析
10、象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图，是一局象棋残局，若“帅”位于点 $(- 1, - 2)$ ， “马”位于 $(3, - 2)$ ，则位于原点位置的是（）

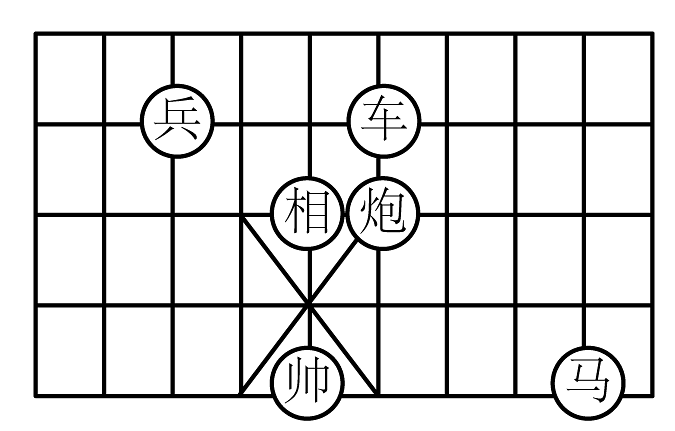A、相 B、炮 C、车 D、兵

查看解析
11、如图，Rt∠COD的顶点O在直线AB上。图中有没有互余的角?为什么?

查看解析
12、一副三角板按图中的四个位置摆放，则其中∠α和 $∠ β$ 具有怎样的数量关系? 分别是互余、互补还是相等?

查看解析
13、如图，已知∠α。利用三角尺画出下列各角。

(1)、∠α的补角；

(2)、∠α的余角。

查看解析
14、判断下列说法是否正确，并说明理由。

(1)、一个锐角的补角一定是钝角；

(2)、如果两个角互补，那么这两个角中，一个是锐角，另一个是钝角；

(3)、如果一个角的余角和补角都存在，那么这个角的余角一定比这个角的补角小。

查看解析
15、如图，射线OA表示北偏西30°（一般不说成“西偏北60°”）方向，你能用类似的方法画图表示下列各方向吗?

（1）北偏东40°；（2）南偏西50°（一般不说成“西偏南40°”）；（3）东南方向（即南偏东45°）。
画出上述方向后，请用数字或希腊字母标注图中互余或互补的角，并把它们列举出来（只需分别列举出两对）。

查看解析
16、

(1)、已知∠α的余角是∠α的2倍，求∠α的度数。

(2)、已知∠1的补角是∠1的3倍，求∠1的度数。

查看解析
17、如图，吊桥桥面与铅垂方向所成的角 $∠ α = 30 °$ 若要把吊桥放平，则吊桥需沿什么方向转动? 转动多少度?

查看解析
18、已知∠α=60°32°，∠α的余角是多少度? ∠α的补角是多少度?

查看解析
19、已知一个角的补角是这个角的余角的4倍，求这个角的度数。

查看解析
20、如图，已知∠AOC=∠BOD=Rt∠。指出图中还有哪些角相等，并说明理由。

查看解析

上一页 94 95 96 97 98 下一页跳转