相关试卷
- 【培优练】人教版初中数学八年级下册 17.1 勾股定理
- 【基础练】人教版数学八年级下学期 17.1 勾股定理
- 【培优练】人教版数学八年级下学期 18.2.1 矩形
- 【基础练】人教版数学八年级下学期 18.2.1 矩形
- 【培优练】人教版数学八年级下学期 18.1平行四边形
- 【基础练】人教版数学八年级下学期 18.1平行四边形
- 人教版数学八年级下学期期中质量检测三(范围:第十六章~第十八章)
- 人教版数学八年级下学期期中质量检测二(范围:第十六章~18.1)
- 人教版数学八年级下学期期中质量检测一(范围:第十六章~18.1)
- 新人教版七年级下学期数学第二次阶段性质量检测(高阶)(考试范围:第七—十章)
-
1、如图, .
 (1)、求证:
(1)、求证:证明: ,
(__________)(_________________)
, (__________)(_________________),
(_________________).
(2)、若是的平分线, , 求的度数. -
2、如图,在平面直角坐标系中,已知的三个顶点坐标分别为 , , .
 (1)、将向右平移4个单位长度,再向下平移2个单位长度后得到 , 请画出;(2)、直接写出点 , , 的坐标;(3)、求的面积.
(1)、将向右平移4个单位长度,再向下平移2个单位长度后得到 , 请画出;(2)、直接写出点 , , 的坐标;(3)、求的面积. -
3、解不等式组 .
-
4、计算: .
-
5、关于的不等式组无解,则字母的取值范围是
-
6、若m,n是两个连续的整数且 , 则.
-
7、如图,在一块长为 , 宽为的长方形草地上,有一条弯曲的小路,小路的左边线向右平移就是它的右边线,则这块草地的绿地面积为 .

-
8、是二元一次方程的一个解,则的值为 .
-
9、若二排三列用有序实数对来表示,则表示五排一列的有序实数对为 .
-
10、某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知 , , , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、平面直角坐标系中,点在x轴上,则m的值为( )A、 B、0 C、2 D、3
-
12、如图,与是一对( )
 A、同位角 B、内错角 C、同旁内角 D、对顶角
A、同位角 B、内错角 C、同旁内角 D、对顶角 -
13、如图,已知:射线交于E, .
 (1)、求证: .(2)、如图2,Y为射线上一动点,直接写出之间的数量关系.(3)、如图3,在(2)的条件下,连接 , 延长交射线于W,N为线段上一动点,若平分 , 平分时,求的值.
(1)、求证: .(2)、如图2,Y为射线上一动点,直接写出之间的数量关系.(3)、如图3,在(2)的条件下,连接 , 延长交射线于W,N为线段上一动点,若平分 , 平分时,求的值. -
14、【数学问题】解方程组
【思路分析】小明观察后发现可以把视为一个整体,把方程①直接代入到方程②中,这样,就可以将方程②直接转化为一元一次方程,从而达到“消元”的目的.
(1)、【完成解答】请你按照小明的思路,完成解方程组的过程.(2)、【迁移运用】请你按照小明的方法,解方程组 -
15、某商场用6600元购进A品牌取暖器和B品牌取暖器共100台,已知A品牌取暖器每台进价为60元,售价为80元;B品牌取暖器每台进价为70元,售价为100元.(1)、两种取暖器各购进多少台?(2)、在将两种取暖器从厂家运往商场的过程中,A品牌取暖器损坏了5台(损坏后的产品只能为废品,不能再进行销售),而B品牌取暖器完好无损,商场决定对这两种取暖器的售价进行调整,使这次购进的取暖器全部售完后,商场可获利 , 已知B品牌取暖器在原售价基础上提高 , 问A品牌取暖器调整后的每台售价比原售价多多少元?
-
16、解方程组:(1)、;(2)、
-
17、如图,已知 , , , 若 , 则 .

-
18、若关于、的二元一次方程组的解为 , 则关于、的二元一次方程组的解为 .
-
19、光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中的平行光线,在空气中也是平行的.如图,若 , 则与的度数和是 .
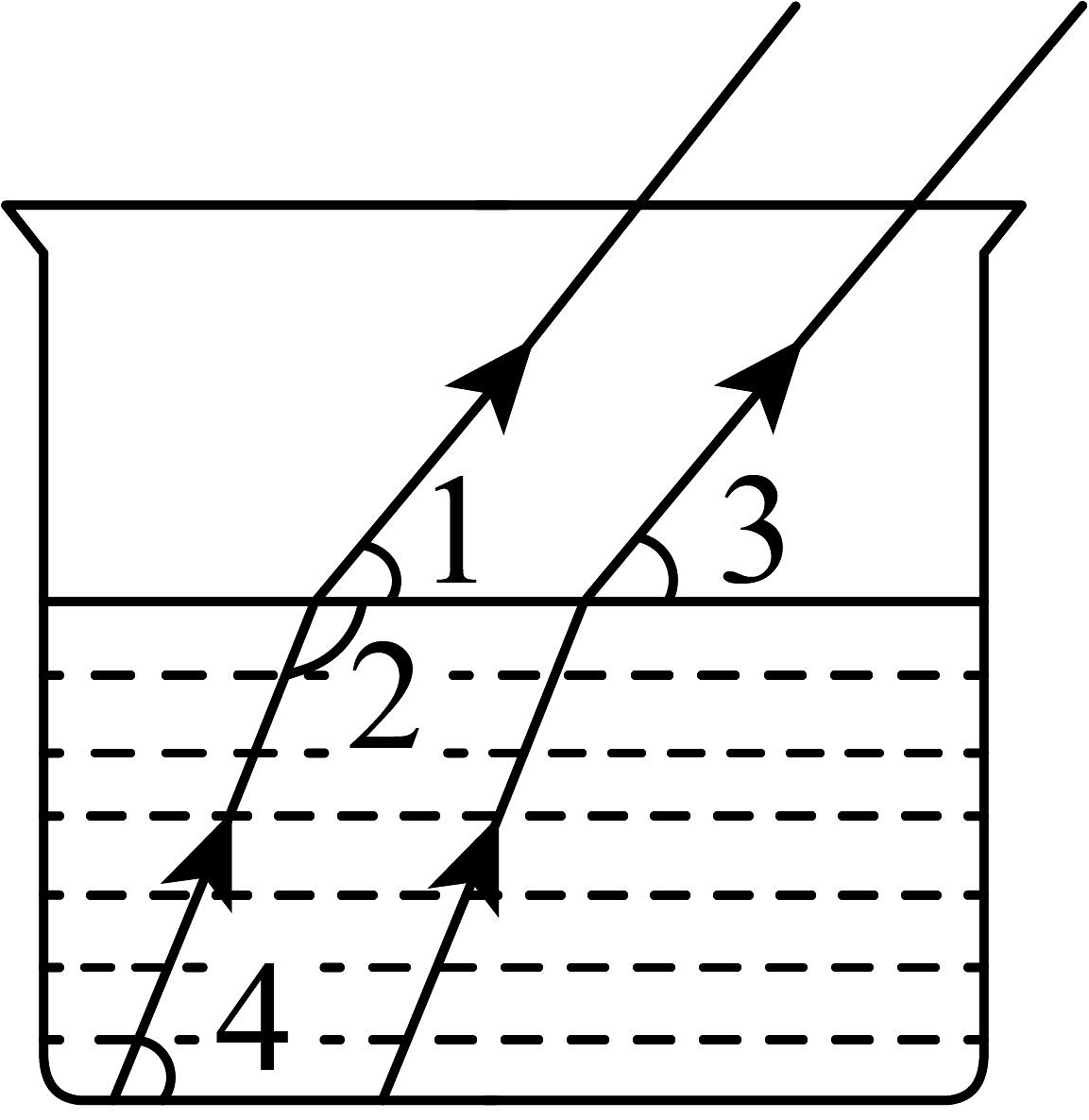
-
20、二元一次方程组用代入消元法消去未知数x,得到关于y的一元一次方程可以是 .