相关试卷

1、在等边△ABC中，点P从点A开始沿边AB匀速运动，点Q从点C开始沿射线BC匀速运动，且P，Q的速度相等，连接PQ交AC于点E，过点P作PD丄AC于D

(1)、求证：DE= $\frac{1}{2}$ ?

(2)、当AB=10，AP=2时求△PDE的面积

查看解析
2、如图，已知平行四边形ABCD，连接对角线AC，BD交于点E，过点E作PQ⊥MN，分别与AB，BC，CD，DA交于点P，M，Q，N．

(1)、求证：ΔDEQ≅ΔBEP ．．

(2)、若依次连接P，M，Q，N，四边形PMQN是什么特殊四边形？说明理由

查看解析
3、已知：如图，在Rt△ABC中，∠C＝90°，AC＝3cm，BC＝4cm，点P从点B出发，沿BC向点C匀速运动，速度为1cm/s；同时，点Q从点A出发，沿AB向点B匀速运动，速度为2cm/s；当一个点停止运动时，另一个点也停止运动连接PQ，设运动时间为t（s）（0＜t＜2.5），解答下列问题：

(1)、①BQ＝ ▲ ， BP＝ ▲ ；（用含t的代数式表示）
②设△PBQ的面积为y（cm2），试确定y与t的函数关系式；

(2)、在运动过程中，是否存在某一时刻t，使△PBQ的面积为△ABC面积的二分之一？如果存在，求出t的值；不存在，请说明理由；

(3)、在运动过程中，是否存在某一时刻t，使△BPQ为等腰三角形？如果存在，求出t的值；不存在，请说明理由．

查看解析
4、如图1，在△ABC中，BE平分∠ABC，CF平分∠ACB，BE与CF交于点D．

(1)、若∠BAC＝74°，则∠BDC＝；

(2)、如图2，∠BAC＝90°，作MD⊥BE交AB于点M，求证：DM＝DE；

(3)、如图3，∠BAC＝60°，∠ABC＝80°，若点G为CD的中点，点M在直线BC上，
连接MG，将线段GM绕点G逆时针旋转90°得GN，NG＝MG，连接DN，当DN最短时，直接写出∠MGC的度数．

查看解析
5、用如图①，②所示的两个直角三角形（部分边长及角的度数在图中已标出），完成以下两个探究问题：

(1)、探究一：将以上两个三角形如图③拼接（BC和ED重合），在BC边上有一动点P．
①当点P运动到∠CFB的角平分线上时，连接AP，求线段AP的长；
②当点P在运动的过程中出现PA=FC时，求∠PAB的度数．

(2)、探究二：如图④，将△DEF的顶点D放在△ABC的BC边上的中点处，并以点D为旋转中心旋转△DEF，使△DEF的两直角边与△ABC的两直角边分别交于M、N两点，连接MN．在旋转△DEF的过程中，△AMN的周长是否存在有最小值？若存在，求出它的最小值；若不存在，请说明理由．

查看解析
6、如图，已知四边形ABCD是矩形，点E在BA的延长线上，AE=AD，EC与BD相交于点G，与AD相交于点F，AF=AB.

(1)、求证：BD⊥EC；

(2)、若AB=1，求AE的长；

(3)、如图，连接AG，求证：EG-DG= $\sqrt{2}$ AG

查看解析
7、如图，在△ABC中，D是BC边上一点，E是AD的中点，过A作BC的平行线交CE的延长线F，且AF＝BD，连接BF．

(1)、求证：点D是BC的中点；

(2)、如果AB＝AC，试判断四边形AFBD的形状，并证明你的结论；

(3)、在（2）的条件下，当△ABC满足什么条件时，四边形AFBD为正方形，并说明理由．

查看解析
8、如图①，在 $△ A B C$ 中， $A B = A C, ∠ B A C = 6 0^{°}, D$ 为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转 $6 0^{°}$ 得到AE，连接EC，则：

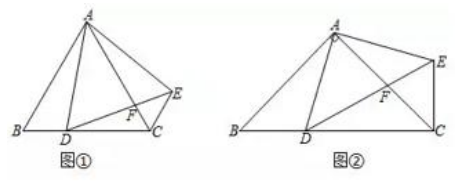(1)、① $∠ A C E$ 的度数是；②线段AC，CD，CE之间的数量关系；

(2)、如图②，在 $△ A B C$ 中， $A B = A C, ∠ B A C = 9 0^{°}, D$ 为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转 $9 0^{°}$ 得到AE，连接EC，请判断线段AC，CD，CE之间的数量关系，并说明理由；

(3)、如图②，AC与DE交于点 $F$ ，在（2）条件下，若 $A C = 8$ ，求AF的最小值．

查看解析
9、如图，在△ABC中，AB=AC，点D是线段BC上一点（包括端点B，C），过点D作DE丄BC交直线AB于E点，交直线AC于点F，设BD=x，

(1)、判断DF+DE的值是否随x的变化而变化，如果不变，请说明理由，如果变化，写出DF+DE与x的关系式

(2)、当x=12时DE达到最大值等于10，求DE+DF的值

查看解析
10、如图，正方形ABCD中，点E在边AD上（不与端点A，D重合），点A关于直线BE的对称点为点F，连接CF，设∠ABE＝α．

(1)、求∠BCF的大小（用含α的式子表示）；

(2)、过点C作CG⊥直线AF，垂足为G，连接DG．判断DG与CF的位置关系，并说明理由；

(3)、将△ABE绕点B顺时针旋转90°得到△CBH，点E的对应点为点H，连接BF，HF．当△BFH为等腰三角形时，求sinα的值．

查看解析
11、如图

(1)、某学校“智慧方园”数学社团遇到这样一个题目：
如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=3 $\sqrt{3}$ ， BO：CO=1：3，求AB的长．
经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．
请回答：∠ADB= ， AB= ．

(2)、请参考以上解决思路，解决问题：
如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=3 $\sqrt{3}$ ， ∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长

查看解析
12、如图，在正方形ABCD的边BC上取点E，边CD的延长线上取点F，使得BE=DF

(1)、求证：ABEΔ≅ΔADF；

(2)、连接EF与AD交于点 $G$ ，若 $B E = 2, t a n ∠ A F D = 3$ ，求AG的长．

查看解析
13、如图

(1)、证明推断：如图（1），在正方形ABCD中，点E、Q分别在边BC，AB上， $D Q ⊥ A E$ 于点 $O$ ，点G、F分别在边CD、AB上， $G F ⊥ A E$ ．
①填空：DQ $A E ($ 填＂ $> "$ ＂<＂或＂＝＂）；②推断 $\frac{G F}{A E}$ 的值为；

(2)、类比探究：如图（2），在矩形ABCD中， $\frac{B C}{A B} = k$ （ $k$ 为常数）．将矩形ABCD沿GF折叠，使点 $A$ 落在BC边上的点 $E$ 处，得到四边形FEPG，EP交CD于点 $H$ ，连接AE交GF于点 $O$ ．试探究GF与AE之间的数量关系，并说明理由；

(3)、拓展应用：在(2)的条件下，连接CP，当当 $k = \frac{2}{3}$ 时，若 $\frac{B E}{B F} = \frac{3}{4}, G F = 2 \sqrt{10}$ ，求CP的长．

查看解析
14、如图，在△ABC与△DEF中，∠ACB＝∠EDF＝90°，BC＝AC ， ED＝FD ，点D在AB上．

(1)、如图1，若点F在AC的延长线上，连接AE ，探究线段AF、AE、AD之间的数量关系，并证明你的结论；

(2)、如图2，若点 $D$ 与点 $A$ 重合，且 $A C = 3 \sqrt{2}, D E = 4$ ，将 $△ D E F$ 绕点 $D$ 旋转，连接BF，点 $G$ 为BF的中点，连接CG，在旋转的过程中，求 $\frac{3}{2} C G + B G$ 的最小值；

(3)、如图3，若点 $D$ 为AB的中点，连接BF，~CE交于点M，CE交AB于点 $N$ ，且BC： $D E : M E = 7 : 9 : 10$ ，请直接写出 $\frac{N D}{C N}$ 的值．

查看解析
15、如图

(1)、问题提出：
如图①，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝23，则∠A的大小为；

(2)、问题探究：如图②，在四边形ABCD中，AD∥BC ，对角线AC与BD相交于O ．若AC＝8，BD＝6，∠AOD＝60°，求四边形ABCD的面积；

查看解析
16、如图

(1)、阅读理解：问题：如图1，在四边形ABCD中，对角线BD平分∠ABC ， ∠A+∠C＝180°．求证：DA＝DC ．
思考：“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题．
方法l：在BC上截取BM＝BA ，连接DM ，得到全等三角形，进而解决问题；
方法2：延长BA到点N ，使得BN＝BC ，连接DN ，得到全等三角形，进而解决问题．
结合图1，在方法1和方法2中任选一种，添加辅助线并完成证明．

(2)、问题解决：如图2，在（1）的条件下，连接AC ，当∠DAC＝60°时，探究线段AB ， BC ， BD之间的数量关系，并说明理由；

(3)、问题拓展：如图3，在四边形ABCD中，∠A+∠C＝180°，DA＝DC ，过点D作
DE⊥BC ，垂足为点E ，请直接写出线段AB、CE、BC之间的数量关系．

查看解析
17、如图，一次函数y= $- \frac{4}{3}$ x+4的图象与x轴和y轴分别交于点B和点A ，以AB为边在第一象限内作正方形ABCD ．

(1)、求AB的长；

(2)、求点C、点D的坐标；

(3)、过点D的直线交x轴于点P ，当△PBC为等腰三角形时，求直线DP的解析式．

查看解析
18、把两块全等的直角三角形ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，其中∠ABC＝∠DEF＝90°，∠C＝∠F＝45°，AB＝DE＝4，把三角板ABC固定不动，让三角板DEF绕点O旋转，设射线DE与射线AB相交于点P ，射线DF与线段BC相交于点Q ．

(1)、如图，当射线DF经过点 $B$ ，即点 $Q$ 与点 $B$ 重合时，易证 $△ A P D ~ △ C D Q$ ．此时， $A P \cdot C Q =$ .

(2)、将三角板DEF由图所示的位置绕点 $O$ 沿逆时针方向旋转，设旋转角为a．其中 $0^{°} < a < 9 0^{°}$ ，问 $A P \cdot C Q$ 的值是否改变？说明你的理由．

(3)、在（2）的条件下，设 $2 < x < 4$ ，两块三角板重叠面积为 $y$ ，求 $y$ 与 $x$ 的函数关系式．

查看解析
19、在等腰 $△ A D E$ 中， $A E = D E, △ A B C$ 是直角三角形， $∠ C A B = 9 0^{°}$ ， $∠ A B C = \frac{1}{2} ∠ A E D$ ，连接CD，~BD，点 $F$ 是BD的中点，连接EF．

(1)、当 $∠ E A D = 4 5^{°}$ ，点 $B$ 在边AE上时，如图（1）所示，求证： $E F = \frac{1}{2} C D$ ；

(2)、当 $∠ E A D = 4 5^{°}$ ，把 $△ A B C$ 绕点 $A$ 逆时针旋转，顶点 $B$ 落在边AD上时，如图（2）所示，当 $∠ E A D = 6 0^{°}$ ，点 $B$ 在边AE上时，如图（3）所示，猜想图（2），图（3）中线段EF和CD又有怎样的数量关系？请直接写出你的猜想，不需证明．

查看解析
20、顶点A在y的正半轴上，OA＝2，一动点E从（3，0）出发，以每秒1个单位的速度沿CB向左运动，到达OB的中点停止．另一动点F从点C出发，以相同的速度沿CB向左运动，到达点O停止．已知点E、F同时出发，以EF为边作正方形EFGH ，使正方形EFGH和△ABC在BC的同侧，设运动的时间为t秒（t≥0）．

(1)、当点H落在AC边上时，求t的值；

(2)、设正方形EFGH与△ABC重叠面积为S ，请问是否存在t值，使得S＝ $\frac{91}{36}$ ？若存在，求出t值；若不存在，请说明理由；

(3)、如图2，取AC的中点D ，连结OD ，当点E、F开始运动时，点M从点O出发，以每秒2 $\sqrt{5}$ 个单位的速度沿OD﹣DC﹣CD﹣DO运动，到达点O停止运动．请问在点E的整个运动过程中，点M可能在正方形EFGH内（含边界）吗？如果可能，求出点M在正方形EFGH内（含边界）的时长；若不可能，请说明理由．

查看解析

上一页 103 104 105 106 107 下一页跳转