安徽省滁州市全椒县2017年中考数学三模试卷
试卷日期:2017-12-07 考试类型:中考模拟
一、选择题
-
1. 实数﹣ 的绝对值是( )A、5 B、 C、﹣ D、﹣2. 下列计算正确的是( )A、 × = B、x8÷x2=x4 C、(2a)3=6a3 D、3a5•2a3=6a63. 因式分解x2y﹣4y的结果是( )A、y(x2﹣4) B、y(x﹣2)2 C、y(x+4)(x﹣4) D、y(x+2)(x﹣2)4. 将一根圆柱形的空心钢管任意放置,它的主视图不可能是( )A、
 B、
B、 C、
C、 D、
D、 5. 某校九年级共有1、2、3、4四个班,现从这四个班中随机抽取两个班进行一场篮球比赛,则恰好抽到1班和2班的概率是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、
5. 某校九年级共有1、2、3、4四个班,现从这四个班中随机抽取两个班进行一场篮球比赛,则恰好抽到1班和2班的概率是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、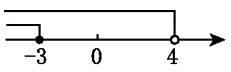 B、
B、 C、
C、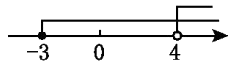 D、
D、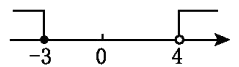 7. 如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )
7. 如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )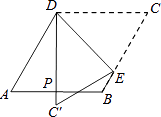 A、78° B、75° C、60° D、45°8. 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A、78° B、75° C、60° D、45°8. 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( ) A、44° B、66° C、88° D、92°9. 如图,AC,BD相交于点O,且OA=OC=4,OB=OD=6,P是线段BD上一动点,过点P作EF∥AC,与四边形的两条边分别交于点E,F,设BP=x,EF=y,则下列能表示y与x之间函数关系的图象是( )
A、44° B、66° C、88° D、92°9. 如图,AC,BD相交于点O,且OA=OC=4,OB=OD=6,P是线段BD上一动点,过点P作EF∥AC,与四边形的两条边分别交于点E,F,设BP=x,EF=y,则下列能表示y与x之间函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )
10. 如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( ) A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
11. 我国计划在2020年左右发射火星探测卫星.据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为千米.12. 若x2﹣3y﹣5=0,则6y﹣2x2﹣6= .13. 如图,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE,PF,PG,PH,则△PEF和△PGH的面积和等于 .
 14. 如图,边长为2的正方形ABCD内接于⊙O,点E是 上一点(不与A、B重合),点F是 上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
14. 如图,边长为2的正方形ABCD内接于⊙O,点E是 上一点(不与A、B重合),点F是 上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:① = ;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④若BG=1﹣ ,则BG,GE, 围成的面积是 + .
其中正确的是(把所有正确结论的序号都填上)

三、综合题
-
15. 计算:( +1)0﹣2﹣1+ ﹣6sin60°.16. 观察下列等式:
① + ﹣ = ;
② + ﹣ = ;
③ + ﹣ = ;
④ + ﹣ = ;
…
(1)、请按以上规律写出第⑤个等式:;(2)、猜想并写出第n个等式:;(3)、请证明猜想的正确性.17. 如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
①画出与△ABC关于y轴对称的△A1B1C1 , 求点C1的坐标。
②以原点O为位似中心,在第四象限画一个△A2B2C2 , 使它与△ABC位似,并且△A2B2C2与△ABC的相似比为2:1.
18. 如图,我东海舰队的一艘军舰在海面A处巡逻时发现一艘不明国籍的船只在C处游弋,立即通知在B处的另一艘军舰一起向其包抄,此时B在A的南偏西30°方向,我两艘军舰分别测得C在A的南偏东75°方向和C在B的北偏东75°方向,已知A,B之间的距离是30海里,求此刻我两艘军舰所在地A,B与C的距离.(结果保留根号) 19. 某校为了美化校园计划购买茶花、桂花两种树苗共600株,茶花树苗每株35元,桂花树苗每株40元.相关资料表明:茶花、桂花树苗的成活率分别为80%,90%.(1)、若购买这两种树苗共用去22000元,则茶花、桂花树苗各购买多少株?(2)、若要使这批树苗的总成活率不低于85%,则茶花树苗至多购买多少株?(3)、在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.20. 某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
19. 某校为了美化校园计划购买茶花、桂花两种树苗共600株,茶花树苗每株35元,桂花树苗每株40元.相关资料表明:茶花、桂花树苗的成活率分别为80%,90%.(1)、若购买这两种树苗共用去22000元,则茶花、桂花树苗各购买多少株?(2)、若要使这批树苗的总成活率不低于85%,则茶花树苗至多购买多少株?(3)、在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.20. 某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.造成医患关系紧张的原因(单选)
A.药价高
B.检测项目太多且收费太高
C.住院报销比例低
D.医疗费与个人收入不相称
E.其他
根据调查结果绘制出了如下两幅尚不完整的统计图.

根据以上信息解答下列问题:
(1)、这次接受调查的总人数为人;(2)、在扇形统计图中,“A”所在扇形的圆心角的度数为;(3)、补全条形统计图;(4)、若该市有1000万人,请你估计选D的总人数.21. 如图,直线AB经过x轴上的点M,与反比例函数y= (x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P. (1)、求k的值;(2)、若AB=2BM,求△ABD的面积;
(1)、求k的值;(2)、若AB=2BM,求△ABD的面积;
(3)、若四边形ABCD为菱形,求直线AB的函数解析式.22. 如图 (1)、问题:如图①,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
(1)、问题:如图①,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证:AD•BC=AP•BP.
(2)、探究:如图②,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ,上述结论是否依然成立?说明理由.
(3)、应用:请利用(1)(2)获得的经验解决问题:如图③,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A,设点P的运动时间为t秒,当以D为圆心,以DC为半径的圆与AB相切时,求t的值.
23. 已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0). (1)、当h=1,k=2时,求抛物线的解析式;(2)、若抛物线y=tx2(t≠0)也经过点A,过a与t之间的关系式;(3)、在(2)的条件下,已知a=﹣ ,直线l:y= x﹣1与抛物线y=tx2﹣ x﹣7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2﹣ x﹣7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值.
(1)、当h=1,k=2时,求抛物线的解析式;(2)、若抛物线y=tx2(t≠0)也经过点A,过a与t之间的关系式;(3)、在(2)的条件下,已知a=﹣ ,直线l:y= x﹣1与抛物线y=tx2﹣ x﹣7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2﹣ x﹣7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值.