安徽省合肥五十中新区2017-2018学年九年级上学期数学开学考试试卷

试卷日期：2017-12-20 考试类型：开学考试

前去【出卷网】下载

一、选择题

1. 下列根式中是最简二次根式的是（）

A、 $\sqrt{\frac{2}{3}}$ B、 $\sqrt{3}$ C、 $\sqrt{9}$ D、 $\sqrt{12}$

查看试题解析
2. 如果反比例函数y= $\frac{2 - k}{x}$ 的图象经过点（﹣1，﹣2），则k的值是（）

A、4 B、0 C、﹣3 D、﹣4

查看试题解析
3. 若把x²+2x﹣2=0化为（x+m）²+k=0的形式（m，k为常数），则m+k的值为（）

A、﹣2 B、﹣4 C、2 D、4

查看试题解析
4. 将抛物线y=x²+2先向左平移1个单位，再向下平移3个单位，所得的抛物线解析式是（）

A、y=（x+1）²+1 B、y=（x+1）²﹣1 C、y=（x﹣1）²﹣1 D、y=（x-1）²+1

查看试题解析
5. 如图，在5×5的正方形网格中，从在格点上的点A，B，C，D中任取三点，所构成的三角形恰好是直角三角形的个数为（）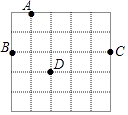

A、1 B、2 C、3 D、4

查看试题解析
6. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：
甲
乙
丙
丁
平均数（cm）
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 如图，数轴上点A，B分别对应1，2，过点B作PQ⊥AB，以点B为圆心，AB长为半径画弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，则点M对应的数是（）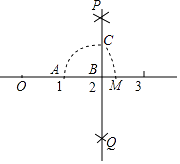

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{6}$ D、 $\sqrt{7}$

查看试题解析
8. 下列函数中，当x＞0时，y随x的增大而增大的是（）

A、y=﹣2x+1 B、y=﹣x²﹣1 C、y=（x+1）²﹣1 D、y= $\frac{1}{x}$

查看试题解析
9. 在▱ABCD中，AB=3，BC=4，当▱ABCD的面积最大时，下列结论正确的有（　　）
①AC=5；②∠A+∠C=180°；③AC⊥BD；④AC=BD．

A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析
10. a，b，c为常数，且（a﹣c）²＞a²+c² ，则关于x的方程ax²+bx+c=0根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、有一根为0

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{2 - x}$ 有意义，则x的取值范围是．

查看试题解析
12. 若x=2是关于x的方程x²﹣4mx﹣8=0的一个根，则m的值为．

查看试题解析
13. 一组数据2，4，a，7，7的平均数 $\bar{x}$ =5，则方差S²= ．

查看试题解析
14. 在菱形ABCD中，E，F分别是AD，BD的中点，若EF=2，则菱形ABCD的周长是．

查看试题解析
15. 抛物线y=﹣x²+3x+4在x轴上截得的线段长度是．

查看试题解析
16. 如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点H处，点D落在点G处，有以下四个结论：
①四边形CFHE是菱形；
②EC平分∠DCH；
③线段BF的取值范围为3≤BF≤4；
④当点H与点A重合时，EF=2 $\sqrt{5}$ ．
以上结论中，你认为正确的有．（填序号）

查看试题解析

三、解答题

17. 计算题

(1)、计算： $\sqrt{3}$ （ $\sqrt{2}$ + $\sqrt{3}$ ）﹣ $\sqrt{24}$

(2)、解方程：x²﹣2x=4．

查看试题解析
18. 如图，已知一次函数y₁=kx+b（k≠0）的图象与反比例函数y₂=﹣ $\frac{8}{x}$ 的图象交于A、B两点，与坐标轴交于M、N两点．且点A的横坐标和点B的纵坐标都是﹣2．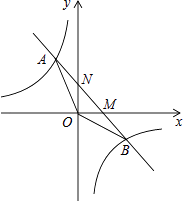

(1)、求一次函数的解析式；

(2)、求△AOB的面积；

(3)、观察图象，直接写出y₁＞y₂时x的取值范围．

查看试题解析
19. 已知关于x的一元二次方程x²+（2m﹣1）x+m²=0有两个实数根x₁和x₂ ．

(1)、求实数m的取值范围；

(2)、当 $x_{1}^{2} - x_{2}^{2} = 0$ 时，求m的值．

查看试题解析
20. 如图，Rt△ABC中，∠ACB=90°，AC边上的垂直平分线交AC于D，交AB于E，延长DE到F，使BF=CE

(1)、四边形BCEF是平行四边形吗？说说你的理由．

(2)、当∠A等于多少时，四边形BCEF是菱形，并说出你的理由．

(3)、四边形BCEF可以是正方形吗？为什么？

查看试题解析
21. 随着智能手机的普及，微信抢红包已成为春节期间人们最喜欢的活动之一，某校七年级（1）班班长对全班50名学生在春节期间所抢的红包金额进行统计，并绘制成了统计图．
请根据以上信息回答：

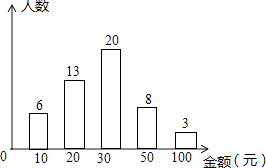(1)、该班同学所抢红包金额的众数是，中位数是；

(2)、该班同学所抢红包的平均金额是多少元？

(3)、若该校共有18个班级，平均每班50人，请你估计该校学生春节期间所抢的红包总金额为多少元？

查看试题解析
22. 某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成，已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边的长为x米．

(1)、若苗圃园的面积为72平方米，求x；

(2)、若平行于墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由；

(3)、当这个苗圃园的面积不小于100平方米时，直接写出x的取值范围．

查看试题解析

	甲	乙	丙	丁
平均数（cm）	185	180	185	180
方差	3.6	3.6	7.4	8.1