安徽省合肥四十五中2017年中考数学一模试卷
试卷日期:2017-11-07 考试类型:中考模拟
一、选择题
-
1. 下列四个实数最小的是( )A、﹣ B、﹣ C、0 D、﹣12. 每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.0000105m,该数值用科学记数法表示为( )A、1.05×105 B、1.05×10﹣5 C、0.105×10﹣5 D、10.5×10﹣43. 将一个长方体内部挖去一个圆柱(如图所示),它的主视图是( )
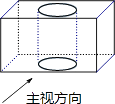 A、
A、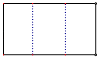 B、
B、 C、
C、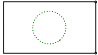 D、
D、 4. 下列计算正确的是( )A、2x2+3x2=5x4 B、(﹣x2)3=﹣x6 C、(x﹣y)2=x2﹣y25. “国庆黄金周”期间,小东和爸爸、妈妈外出旅游,一家三人随机站在一排拍照纪念,小东恰好站在中间的概率是( )A、 B、 C、 D、6. 将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )
4. 下列计算正确的是( )A、2x2+3x2=5x4 B、(﹣x2)3=﹣x6 C、(x﹣y)2=x2﹣y25. “国庆黄金周”期间,小东和爸爸、妈妈外出旅游,一家三人随机站在一排拍照纪念,小东恰好站在中间的概率是( )A、 B、 C、 D、6. 将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )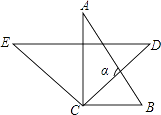 A、105° B、115° C、95° D、110°7. 如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )
A、105° B、115° C、95° D、110°7. 如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )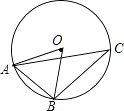 A、π B、 C、 D、8. 某市2015年国内生产总值(GDP)比2014年增长了12%,预计2016年比2015年增长7%,若这两年GDP年平均增长率为x%,则x%满足的关系是( )A、12%+7%=x% B、(1+12%)(1+7%)=2(1+x%) C、12%+7%=2x% D、(1+12%)(1+7%)=(1+x%)29. 已知反比例函数y= 的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为( )
A、π B、 C、 D、8. 某市2015年国内生产总值(GDP)比2014年增长了12%,预计2016年比2015年增长7%,若这两年GDP年平均增长率为x%,则x%满足的关系是( )A、12%+7%=x% B、(1+12%)(1+7%)=2(1+x%) C、12%+7%=2x% D、(1+12%)(1+7%)=(1+x%)29. 已知反比例函数y= 的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为( )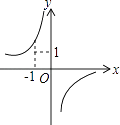 A、
A、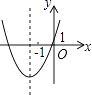 B、
B、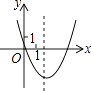 C、
C、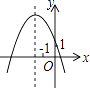 D、
D、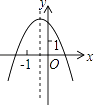 10. 如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
10. 如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( ) A、
A、 B、
B、 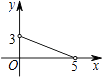 C、
C、 D、
D、
二、填空题
-
11. 能够使代数式 有意义的x的取值范围是 .12. 因式分解: = .13. 定义运算a★b= ,则 ★ =; ★1= .14. 如图,正方形ABCD中,E、F均为中点,则下列结论中:①AF⊥DE;②AD=BP;③PE+PF= PC;④PE+PF=PC.其中正确的是 .

三、解答题
-
15. 先化简,再求值:(a﹣ )÷( ),其中a满足a2﹣3a+2=0.
16. 解不等式组 .四、解答题
-
17. 如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.
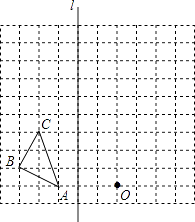
①画出△ABC关于直线l成轴对称的△A0B0C0;
②画出将△A0B0C0向上平移1个单位得到的△A1B1C1;
③以格点O为位似中心,将△A1B1C1作位似变换,将其放大到原来的两倍,得到△A2B2C2 .
18. 如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中心重合,这样得到图②,图③,…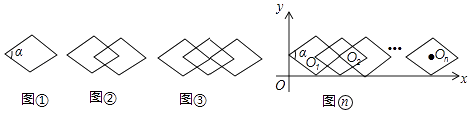 (1)、观察图形并完成表格:
(1)、观察图形并完成表格:图形名称
基本图形的个数
菱形的个数
图①
1
1
图②
2
3
图③
3
7
图④
4
…
…
…
猜想:在图n中,菱形的个数为 [用含有n(n≥3)的代数式表示];
(2)、如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为五、解答题
-
19. 某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图.
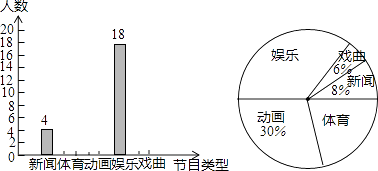
请你根据以上的信息,回答下列问题:
(1)、本次共调查了名学生,其中最喜爱戏曲的有人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是 .(2)、根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.20. 为加强中小学生体育运动,某市第十七届中小学生田径运动会在市体育场举行,体育场主席台侧面如图所示,若顶棚顶端D与看台底端A的连线和地面垂直,测得顶棚CD的长为12米,∠BAC=30°,∠ACD=45°,求看台AC的长.(结果保留一位小数,参考数据: ≈1.41, ≈1.73)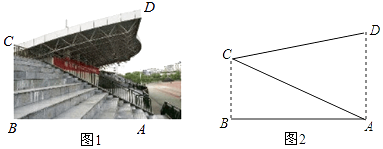
六、解答题
-
21. 如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
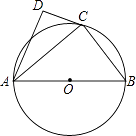 (1)、若BC=3,AB=5,求AC的值;(2)、若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
(1)、若BC=3,AB=5,求AC的值;(2)、若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.七、解答题
-
22. “低碳环保”已经成为一种生活理念,同时也带来无限商机.某高科技发展公司投资2000万元成功研制出一种市场需求量较大的低碳高科技产品.已知生产每件产品的成本是40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利为z(万元).(年获利=年销售额﹣生产成本﹣投资)(1)、试写出z与x之间的函数关系式;(2)、请通过计算说明,到第一年年底,当z取最大值时,销售单价x定为多少?此时公司是盈利了还是亏损了?(3)、若该公司计划到第二年年底获利不低于1130万元,请借助函数的大致图象说明,第二年的销售单价x(元)应确定在什么范围内?
八、解答题
-
23. 在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.
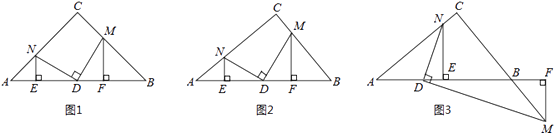 (1)、特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;(2)、拓展探究:若AC≠BC.
(1)、特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;(2)、拓展探究:若AC≠BC.①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明.
-
-