相关试卷

1、下列各式中，正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\pm \sqrt{9} = 3$ C、 $\sqrt{- 9} = - 3$ D、 $\sqrt{{(- 16)}^{2}} = 16$

查看解析
2、如图所示：若m∥n，∠1=120°，则∠2=（）

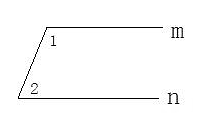A、55° B、60° C、65° D、75°

查看解析
3、如下四个图形中，能由已知图形经过平移得到的是（）

A、 B、 C、 D、

查看解析
4、如图，在 $4 \times 4$ 的正方形网格中，每个小格的顶点叫做格点，设顶点在格点上的三角形为格点三角形，按下列要求画图．

(1)、请你在网格图中画出边长为 $\sqrt{2}$ ， $2 \sqrt{2}$ ， $\sqrt{10}$ 的格点三角形；

(2)、在（1）的条件下，求三角形最长边上的高．

查看解析
5、定义：若 $α - β = 90^{\circ}$ ，且 $90^{\circ} < α < 180^{\circ}$ ，则我们称 $β$ 是 $α$ 的差余角.例如：若 $α = 110^{\circ}$ ，则 $α$ 的差余角 $β = 20^{\circ}$ .

(1)、如图1，点O在直线 $A B$ 上，射线 $O E$ 是 $∠ B O C$ 的角平分线，若 $∠ C O E$ 是 $∠ A O C$ 的差余角，求 $∠ B O E$ 的度数.

(2)、如图2，点O在直线 $A B$ 上，若 $∠ B O C$ 是 $∠ A O E$ 的差余角，那么 $∠ B O C$ 与 $∠ B O E$ 有什么数量关系.

(3)、如图3，点O在直线 $A B$ 上，若 $∠ C O E$ 是 $∠ A O C$ 的差余角，且 $O E$ 与 $O C$ 在直线 $A B$ 的同侧，请你探究 $\frac{∠ A O C - ∠ B O C}{∠ C O E}$ 是否为定值？若是，请求出定值；若不是，请说明理由.

查看解析
6、材料一：解方程组 ${\begin{cases} (a - 1) + 2 (b + 2) = 6 \\ 2 (a - 1) + (b + 2) = 6 \end{cases}$ 时，采用了一种“换元法”的解法，解法如下：
解：设a-1=x ， b+2=y ，原方程组可化为 ${\begin{cases} x + 2 y = 6 \\ 2 x + y = 6 \end{cases}$ ，解得 ${\begin{cases} x = 2 \\ y = 2 \end{cases}$ ，即 ${\begin{cases} a - 1 = 2 \\ b + 2 = 2 \end{cases}$ ，解得 ${\begin{cases} a = 3 \\ b = 0 \end{cases}$
材料二：解方程组 ${\begin{cases} 4 x + 10 y = 6 (1) \\ 8 x + 22 y = 10 (2) \end{cases}$ 时，采用了一种“整体代换”的解法，解法如下：
解：将方程② $8 x + 20 y + 2 y = 10$ 变形为 $2 (4 x + 10 y) + 2 y = 10$ ③，把方程①代入③得，2 $\times$ 6+2y=10，则y=-1；把y=-1代入①得，x=4，所以方程组的解为： ${\begin{cases} x = 4 \\ y = - 1 \end{cases}$ .根据上述材料，解决下列问题：
运用换元法求关于a ， b的方程组 ${\begin{cases} (\frac{a}{4} - 1) + 2 (\frac{b}{3} + 2) = 4 \\ 2 (\frac{a}{4} - 1) + (\frac{b}{3} + 2) = 5 \end{cases}$ 的解；
若关于x ， y的方程组 ${\begin{cases} a_{1}^{} x + b_{1}^{} y = c_{1}^{} \\ a_{2}^{} x + b_{2}^{} y = c_{2}^{} \end{cases}$ 的解为 ${\begin{cases} x = 10 \\ y = 6 \end{cases}$ ，求关于m ， n的方程组 ${\begin{cases} 5 a_{1}^{} (m - 3) + 3 b_{1}^{} (n + 2) = c_{1}^{} \\ 5 a_{2}^{} (m - 3) + 3 b_{2}^{} (n + 2) = c_{2}^{} \end{cases}$ 的解；
已知x ， y ， z满足 ${\begin{cases} 3 x - 2 z + 12 y = 47 \\ 2 x + z + 8 y = 36 \end{cases}$ ，试求z的值.

查看解析
7、阅读下面文字，根据所给信息解答下面问题：把几个数用大括号括起来，中间用逗号隔开，如：{-3，4}，{-3，6，8，18}，其中大括号内的数称其为集合的元素.如果一个集合满足：只要其中有一个元素 $a$ ，使得 $- 2 a + 4$ 也是这个集合的元素，这样的集合称为条件集合.例如；{-3，-2}，因为 $- 2 \times 3 + 4 = - 2$ ， -2恰好是这个集合的元素.所以{3，-2}是条件集合：例如；{-2，9，8}，因为 $- 2 \times (- 2) + 4 = 8$ ， 8恰好是这个集合的元素，所以{-2，9，8}是条件集合.

(1)、集合｛－4，12｝是否是条件集合？

(2)、集合 ${\frac{22}{3}, \frac{1}{2}, - \frac{5}{3}}$ 是否是条件集合？

(3)、若集合 ${8$ ， $n}$ 和 ${m}$ 都是条件集合.求 $m$ 、 $n$ 的值.

查看解析
8、已知： $A = x^{2} + 2 x - 1, B = 3 x^{2} - 2 a x + 1$ .

(1)、用含 $a, x$ 的代数式表示 $3 A - B$ ；

(2)、若 $3 A - B$ 的值与 $x$ 无关，求 $a$ 的值.

查看解析
9、已知2的平方等于 $a$ ， $(2 b - 1)$ 是27的立方根， $\pm \sqrt{c - 2}$ 表示3的平方根，求 $2 a - b + c$ 的值.

查看解析
10、解下列方程(组)：

(1)、106°43^'12″-53.46°（结果用度分秒表示）

(2)、 $- 3^{2} \times 2 + \sqrt{{(- 4)}^{2}} + \sqrt[3]{- 64}$ .

查看解析
11、已知 ${\begin{cases} x = - 2 \\ y = 3 \end{cases}$ 是关于x ， y的方程组 ${\begin{cases} 3 x - 2 a y = 6 \\ b x + 4 y = - 2 \end{cases}$ 的解，则关于x的方程 $a x + b = 1$ 的解是.

查看解析
12、若3x⁵yⁿ与﹣2x^my的和是单项式，则（m﹣n）²的算术平方根是.

查看解析
13、如图，点M在线段AN的延长线上，且线段MN=20，第一次操作：分别取线段AM和AN的中点 $M_{1} ， N_{1}$ ；第二次操作：分别取线段 $A M_{1}$ 和 $A N_{1}$ 的中点 $M_{2}, N_{2}$ ；第三次操作：分别取线段 $A M_{2}$ 和 $A N_{2}$ 的中点 $M_{3}, N_{3}$ ；连续这样操作10次，则每次的两个中点所形成的所有线段之和 $M_{1} N_{1} + M_{2} N_{2} + ⋯ + M_{10} N_{10} =$ （）

A、 $20 - \frac{10}{2^{9}}$ B、 $20 + \frac{10}{2^{9}}$ C、 $20 - \frac{10}{2^{10}}$ D、 $20 + \frac{10}{2^{10}}$

查看解析
14、实数a ， b ， c ， d在数轴上的对应点的位置如图所示，若a+c＝0，则下列结论正确的是（）

A、 $\frac{b}{c} ＞ 0$ B、b+d＞0 C、ad＞bc D、|b|＞|a|

查看解析
15、有m辆客车及n个人，若每辆客车乘40人，则还有10人不能上车；若每辆客车乘43人，则还有1人不能上车.有下列四个等式：① $40 m + 10 = 43 m - 1$ ；② $\frac{n + 10}{40} = \frac{n + 1}{43}$ ；③ $\frac{n - 10}{40} = \frac{n - 1}{43}$ ；
④ $40 m + 10 = 43 m + 1$ .其中正确的是（）

A、①② B、②④ C、②③ D、③④

查看解析
16、若∠1，∠2互为余角，且∠1>∠2，则∠2的补角是（）

A、2（∠1-∠2） B、2（∠1+∠2） C、2∠1+∠2 D、∠1+2∠2

查看解析
17、下列运算正确的是（）

A、 $- 5 - 3 = - 2$ B、 $3 a b - a b = 2$ C、 $a - (b - c) = a - b + c$ D、 $(- 1)^{2} \div (- 1) = 1$

查看解析
18、下列各式中，符合代数式书写规则的是（）

A、 $- 2 \frac{1}{6} p$ B、 $\frac{7}{3} x^{2}$ C、 $a \times \frac{1}{4}$ D、 $2 y \div x$

查看解析
19、自然数2025的倒数是（）

A、2025 B、-2025 C、 $- \frac{1}{2025}$ D、 $\frac{1}{2025}$

查看解析
20、中国象棋棋盘中蕴含着平面直角坐标系，如图是中国象棋棋盘的一半，棋子“马”走的规则是沿“日”形的对角线走．例如：图①中“马”所在的位置可以直接走到点 $A$ 、 $B$ 处．

(1)、如果“帅”位于点 $(0, 0)$ ， “相”位于点 $(4, 2)$ ，则“马”所在的点的坐标为__________，点 $C$ 的坐标为__________，点 $D$ 的坐标为__________．

(2)、若“马”的位置在 $C$ 点，为了到达 $D$ 点，请按“马”走的规则，在图中画出一种你认为合理的行走路线，并用坐标表示．

查看解析

上一页 21 22 23 24 25 下一页跳转