相关试卷

1、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数 $(V)$ 、面氨 $(F)$ 、面数 $(E)$ 之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：

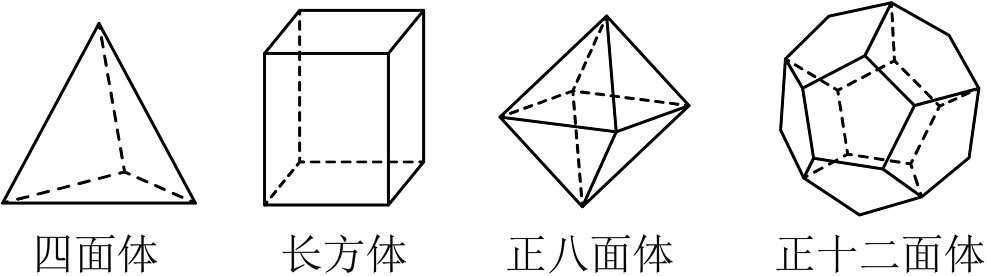(1)、根据上面多面体模型，完成表格中的空格：
多面体
顶点数 $(V)$
面数 $(F)$
棱数 $(E)$
四面体
4
4
_____
长方体
8
6
12
正八面体
_____
8
12
正十二面体
20
12
30

(2)、根据表格，直接写出你发现顶点数 $(V)$ 、函数 $(F)$ 、棱数 $(E)$ 之间存在的关系式_____．

(3)、一个多面体的面数比顶点数大8，且有30条棱，应用（2）的结论，求这个多面体的面数．

查看解析
2、如图，线段 $A B = 8$ ，点 $C$ 是线段 $A B$ 的中点，点 $D$ 是线段 $B C$ 的中点．

(1)、求线段 $A D$ 的长；

(2)、若在线段 $A C$ 上有一点E， $C E = \frac{1}{4} B C$ ，求 $D E$ 的长．

查看解析
3、已知 $x^{2} + 3 x = 2$ ，则多项式 $3 x^{2} + 9 x - 4$ 的值是．

查看解析
4、中国空间站位于距离地面约 $400km$ 的太空环境中．由于没有大气层保护，在太阳光线直射下，空间站表面温度可高于零上 $150 ℃$ ，其背阳面温度可低于零下 $100 ℃$ ．若零上 $150 ℃$ 记作 $+ 150 ℃$ ，则零下 $100 ℃$ 记作 $℃$ ．

查看解析
5、数学源于生活，寓于生活，用于生活．下列各选项中能用“两点之间，线段最短”来解释的现象是（）

A、测量跳远成绩 B、木板上弹墨线 C、弯曲河道改直 D、两钉子固定木条

查看解析
6、若干桶方便面放在桌面上，如图是从正面、左面、上面看到的结果，则这一堆方便面共有（）

A、7桶 B、8桶 C、9桶 D、10桶

查看解析
7、如图，点 $E$ 在线段 $C D$ 的延长线上，下列条件中不能判定 $B D ∥ A C$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3= ∠ 4$ C、 $∠ 5 = ∠ C$ D、 $∠ C + ∠ B D C = 180 °$

查看解析
8、下列几何体中是三棱锥的是（）

A、 B、 C、 D、

查看解析
9、代数式 $\frac{x y}{3}$ 、 $\frac{3}{x}$ 、 $x + y^{2}$ 、 $3 a b$ 、 $- \frac{5}{9} (x^{2} + y^{2})$ ，其中整式有（）

A、2个 B、3个 C、4个 D、5个

查看解析
10、下列代数式中，符合代数式书写要求的是（）

A、 $\frac{m}{n}$ B、 $2 \frac{1}{3} x y$ C、 $2 \div x$ D、 $a \cdot 3$

查看解析
11、 $- 2$ 的相反数是（）

A、 $- 2$ B、2 C、0 D、 $\pm 2$

查看解析
12、已知： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ； $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ； $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ；…

(1)、探索：第n个式子 $\frac{1}{n (n + 1)} =$ ；

(2)、按上述规律计算： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots \dots \frac{1}{9 \times 10}$

(3)、探究并计算： $\frac{1}{2 \times 4} + \frac{1}{4 \times 6} + \frac{1}{6 \times 8} + \dots + \frac{1}{2024 \times 2026}$

查看解析
13、如图，已知线段 $A B$ ，点C与点D在线段 $A B$ 上，若点D为线段 $A B$ 的中点， $A C : C B = 3 : 2$ ， $A C = 6$ ，求线段 $C D$ 的长度．

查看解析
14、若 ${(2 a + 4)}^{2}$ 与 $|2 b - 6|$ 互为相反数．

(1)、求 $a$ ， $b$ 的值；

(2)、规定一种新运算： $x * y = x y + 2$ ，如 $3 * 4 = 3 \times 4 + 2 = 14$ ，求 $a^{2} * (a * b)$ 的值．

查看解析
15、先化简，再求值： $3 x^{2} + 2 (2 x^{2} - 3) - (5 x^{2} - x)$ ，其中 $x = - \frac{1}{2}$ ．

查看解析
16、解方程： $\frac{5 x + 1}{2} - \frac{7 x + 2}{4} = 1$ ．

查看解析
17、计算： $- 2^{2} \times \frac{1}{4} - |- 6| + 9 \div (- 3)$ ．

查看解析
18、如图是由同样大小的小圆圈按一定规律组成的图形，其中第1个图形中共有6个小圆圈，第2个图形中共有9个小圆圈，第3个图形中共有12个小圆圈，按照这样的规律，第n个图形中共有个小圆圈．

查看解析
19、已知关于 $x$ 的方程 $a x + 10 = 7 x - 3$ 的解是正整数，则正整数 $a =$ ．

查看解析
20、如图，一副三角板（直角顶点重合）摆放在桌面上，若 $∠ A O D = 160 °$ ，则 $∠ B O C =$ ．

查看解析

上一页 19 20 21 22 23 下一页跳转

多面体	顶点数 $(V)$	面数 $(F)$	棱数 $(E)$
四面体	4	4	_____
长方体	8	6	12
正八面体	_____	8	12
正十二面体	20	12	30