相关试卷

1、问题情境：如图1，△ABC为等腰直角三角形，∠ACB＝90°，F是AC边上的一个动点（点F与A、C不重合），以CF为一边在等腰直角三角形外作正方形CDEF连接BF、AD ．

(1)、探究展示：
①猜想图1中线段BF、AD的数量关系及所在直线的位置关系，直接写出结论；
②将图1中的正方形CDEF绕着点C按顺时针方向旋转角度α ，得到如图2的情形．图2中BF交AC于点H ，交AD于点O ，请你判断①中得到的结论是否仍然成立，并选取图2证明你的判断．

(2)、拓展延伸：
将原题中的等腰直角三角形ABC改为直角三角形 $A B C, ∠ A C B = 9 0^{°}$ ，正方形CDEF改为矩形CDEF，如图3，且 $A C = 4, B C = 3, C D = \frac{4}{3}, C F = 1, B F$ 交AC于点 $H$ ，交AD于点 $O$ ，连接BD，~AF，求 $B D^{2} + A F^{2}$ 的值．

查看解析
2、如图，已知矩形ABCD中，AB＝4，AD＝m ，动点P从点D出发，在边DA上以每秒1个单位的速度向点A运动，连接CP ，作点D关于直线PC的对称点E ，设点P的运动时间为t（s）．已知m满足：在动点P从点D到点A的整个运动过程中，有且只有一个时刻t ，使点E到直线BC的距离等于3，则所有这样的m的取值范围为.

查看解析
3、如图，在Rt $△ A B C$ 中， $∠ B A C = 9 0^{°}, A C = 2 \sqrt{3}$ ，点0是AB的中点，点 $M$ （不与点 $C$ 重合是射线C0上的一个动点，且 $∠ A O C =$ $6 0^{°}$ ．

(1)、若四边形ACBM是平行四边形，求OM的长；

(2)、当 $△ A B M$ 为直角三角形时，求AM的长；

(3)、设 $O M = x$ ，求 $\frac{A M}{B M}$ 的最大值和最小值．

查看解析
4、如图，在等边△ABC中，点E是边AC上一定点，点D是直线BC上一动点，以DE为边作等边△DEF ，连接CF ．

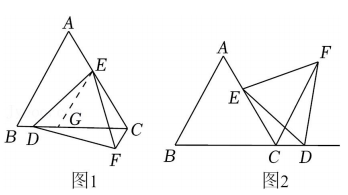(1)、如图1，若点D在边BC上，试说明CE+CF＝CD；（提示：在线段CD上截取CG＝CE ，连接EG ．）

(2)、如图2，若点D在边BC的延长线上，请探究线段CE ， CF与CD之间的数量关系并说明理由

查看解析
5、如图，若 $△ A B C$ 内一点 $P$ 满足 $∠ P A C = ∠ P C B =$ $∠ P B A$ ，则称点P为 $△ A B C$ 的布罗卡尔点，三角形的布罗卡尔点是法国数学教育家克雷尔首次发现，后来被数学爱好者法国军官布罗卡尔重新发现，并用他的名字命名，布罗卡尔点的再次发现，引发了研究＂三角形几何＂的热潮．已知 $△ A B C$ 中， $C A = C B$ ， $∠ A C B = 12 0^{°}, P$ 为 $△ A B C$ 的布罗卡尔点，若 $P B = 3$ ，则 $P A + P C =$ .

查看解析
6、在 $△ A B C$ 中， $A B = A C, ∠ B A C = 2 ∠ D A E = 2 α$ ．

(1)、如图1，若点 $D$ 关于直线AE的对称点为 $F$ ，求证： $△ A D F ~ △ A B C$ ；

(2)、如图2，在（1）的条件下，若 $α = 4 5^{°}$ ，求证： $D E^{2} = B D^{2} + C E^{2}$ ；

(3)、如图3，若 $α = 4 5^{°}$ ，点E在BC的延长线上，则等式 $D E^{2} = B D^{2} + C E^{2}$ 还能成立吗？．请说明理由．

查看解析
7、问题探究：

(1)、如图①，已知等边△ABC，边长为4，则△AB的外接圆的半径长为．

(2)、如图②，在矩形??CD中，?B=4，对角线BD与边BC的夹角为30°，点E在为边BC
上且 $B E = \frac{1}{4} B C$ ，点 $P$ 是对角线BD上的一个动点，连接PE，PC，求 $△ P E C$ 周长的最小值．

(3)、问题解决：为了迎接新年的到来，西安城墙举办了迎新年大型灯光秀表演．其中一个镭射灯距城墙30米，镭射灯发出的两根彩色光线夹角为 $6 0^{°}$ ，如图（3）．若将两根光线 $(A B, A C)$ 和光线与城墙的两交点的连接的线段 $(B C)$ 看作一个三角形，记为 $△ A B C$ ，那么该三角形周长有没有最小值，若有，求出最小值，若没有说明理由．

查看解析
8、如图，四边形ABCD中，AD＝CD ， ∠DAB＝∠ACB＝90°，过点D作DE⊥AC ，垂足为F ， DE与AB相交于点E ．

(1)、求证：AB•AF＝CB•CD

(2)、已知AB＝15cm ， BC＝9cm ， P是射线DE上的动点．设DP＝xcm（x＞0），四边形BCDP的面积为ycm² ．
①求y关于x的函数关系式；
②当x为何值时，△PBC的周长最小，并求出此时y的值．

查看解析
9、如图，在△ABC中，AB＝5，BC＝10，以AC为边构造Rt△ADC ，使得∠ADC＝90°且cos∠ACD＝ $\frac{3}{5}$ ，连接BD ，则BD的最小值为.

查看解析
10、如图，正方形ABCD的边长是4，F点是BC边的中点，点O是CD边上的一个动点，以O点为圆心，OC为半径的圆与CD相交于H点，连接HF交圆O于E点，则线段DE的最小值为.

查看解析
11、如图

(1)、【问题情境】八上《伴你学》第138页有这样一个问题：如图1，把一块三角板（AB＝BC ， ∠ABC＝90°）放入一个“U”形槽中，使三角形的三个顶点A、B、C分别在槽的两壁及底边上滑动，已知∠D＝∠E＝90°，在滑动过程中，你发现线段AD与BE有什么关系？试说明你的结论；

(2)、【变式探究】小明在解决完这个问题后，将其命名为“一线三等角”模型；如图2，在△ABC中，点D、E、F分别在边BC、AC、AB上，若∠B＝∠FDE＝∠C ，则这三个相等的角之间的联系又会使图形中出现其他的一些等角．请你写出其中的一组，并加以说理；

(3)、【拓展应用】如图3，在△ABC中，BA＝BC ， ∠B＝45°，点D、F分别是边BC、AB上的动点，且AF＝2BD ．以DF为腰向右作等腰△DEF ，使得DE＝DF ， ∠EDF＝45°，连接CE ．
①试判断线段DC、BD、BF之间的数量关系，并说明理由；
②如图4，已知AC＝2，点G是AC的中点，连接EA、EG ，直接写出EA＋EG的最小值．

查看解析
12、如图，直线 $y = - \frac{4}{3} x + 8$ 分别与 $x$ 轴， $y$ 轴相交于点 $A$ ，点 $B$ ，作矩形ABCD，其中点 $C$ ，点 $D$ 在第一象限，且满足 $A B : B C = 2 : 1$ ．连接BD．

(1)、求点 $A$ ，点 $B$ 的坐标．

(2)、若点 $E$ 是线段AB（与端点 $A$ 不重合）上的一个动点，过 $E$ 作 $E F / / A D$ ，交BD于点 $F$ ，作直线AF．
①过点 $B$ 作 $B G ⊥ A F$ ，垂足为 $G$ ，当 $B E = B G$ 时，求线段AE的长度．
②若点 $P$ 是线段AD上的一个动点，连结PF，将 $△ D F P$ 沿PF所在直线翻折，使得点 $D$ 的对应点 $D^{ℂ}$ 落在线段BD或线段AB上．直接写出线段AE长的取值范围．

查看解析
13、如图1， $P$ 为第象限内一点，过P，~O两点的 $⊙ M$ 交 $x$ 轴正半轴于点 $A$ ，交 $y$ 轴正半轴于点 $B, ∠ O P A = 4 5^{°}$ ．

(1)、求证：PO平分 $∠ A P B$ ；

(2)、作 $O H ⊥ P A$ 交弦PA于 $H$ ．
①若 $A H = 2, O H + P B = 8$ ，求BP的长；
②若 $B P = m, O H = n$ ，把 $△ P O B$ 沿 $y$ 轴翻折，得到 $△ P^{^{'}} O B$ （如图2），求 $A P^{^{'}}$ 的长．

查看解析
14、如图，矩形ABCD的边 $A B = 3 c m, A D = 4 c m$ ，点 $E$ 从点 $A$ 出发，沿射线AD移动．以CE为直径作 $⊙ O$ ，点 $F$ 为 $⊙ O$ 与射线BD的公共点，连接EF，~CF．过点 $E$ 作 $E G ⊥ E F, E G$ 与 $⊙ O$ 相交于点 $G$ ，连接CG．

(1)、试说明四边形EFCG是矩形；

(2)、当 $⊙ O$ 与射线BD相切时，点 $E$ 停止移动，在点 $E$ 移动的过程中．
①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；
②求点 $G$ 移动路线的长．

查看解析
15、如图，菱形 $A B C D, ∠ A B C = 12 0^{°}$ ，点 $E$ 为平面内一点，连接AE．

(1)、如图1，点 $E$ 在BC的延长线上，将AE绕点 $A$ 顺时针旋转 $6 0^{°}$ 得AF，交EB延长线于点 $G$ ，连接EF交AB延长线于点 $H$ ，若 $∠ A E B = 1 5^{°}, H F = 4$ ，求AE的长；

(2)、如图2，点 $E$ 在AC的延长线上，将AE绕点 $A$ 逆时针旋转 $6 0^{°}$ 得AF，连接EF，点 $M$ 为CE的中点，连接BM，FM，证明： $F M = \sqrt{3} B M$ ；

(3)、如图3，将AB沿AS翻折得 $A E (∠ B A E < 12 0^{°})$ ，连DE交AS于点 $S$ ，点 $T$ 为平面内一点，当DS取得最大值时，连接TD，TE，若 $A T = 3, A D = 6$ ，求 $T D - T E$ 的最大值．

查看解析
16、已知，如图，在平行四边形ABCD中，AB＝3cm ， BC＝5cm ， AC⊥AB ， △ACD沿AC的方向匀速平移得到△PNM ，速度为1cm/s；同时，点Q从点C出发，沿CB方向匀速移动，速度为1cm/s ，当△PNM停止平移时，点Q也停止移动，如图②，设移动时间为t（s）（0＜t＜4），连接PQ ， MQ ， MC ，解答下列问题：

(1)、当t为何值时，PQ∥MN；

(2)、设△QMC的面积为y（cm²），求y与t之间的函数关系式；

(3)、是否存在某一时刻t ，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由．

查看解析
17、如图1，矩形OABC的顶点O是直角坐标系的原点，点A、C分别在x轴、y轴上，点B的坐标为（8，4），将矩形OABC绕点A顺时针旋转得到矩形ADEF ， D、E、F分别与B、C、O对应，EF的延长线恰好经过点C ， AF与BC相交于点Q ．

(1)、证明：△ACQ是等腰三角形；

(2)、求点D的坐标；

(3)、如图2，动点M从点A出发在折线AFC上运动（不与A、C重合），经过的路程为x ，过点M作AO的垂线交AC于点N ，记线段MN在运动过程中扫过的面积为S；求S关于x的函数关系式．

查看解析
18、如图1所示，直角坐标系中，二次函数y＝ax²+bx+6（a≠0）交x轴于A（﹣4，0），B（2，0），在y轴上有点E（0，﹣3）．

(1)、求二次函数的表达式．

(2)、点D是第二象限内的抛物线上一动点，连接AE和DE ．
①连接DC ，当 $\frac{S_{△ D A E}}{S_{△ C D E}} = \frac{1}{3}$ 时，求出点D的坐标；
②当tan∠AED＝ $\frac{6}{7}$ ，求出点D坐标；

(3)、如图3，若点P是直线CA上的动点，连接OP和PE ，当∠OPE最大时，则点P的坐标为.

查看解析
19、已知：如图，在平面直角坐标系中，矩形AOBC的顶点C的坐标是（6，4），动点P从点A出发，以每秒1个单位的速度沿线段AC运动，同时动点Q从点B出发，以每秒2个单位的速度沿线段BO运动，当Q到达O点时，P ， Q同时停止运动，运动时间是t秒（t＞0）．

(1)、如图1，当时间t＝秒时，四边形APQO是矩形；

(2)、如图2，在P ， Q运动过程中，当PQ＝5时，时间t等于秒；

(3)、如图3，当P ， Q运动到图中位置时，将矩形沿PQ折叠，点A ， O的对应点分别是D ， E ，连接OP ， OE ，此时∠POE＝45°，连接PE ，求直线OE的函数表达式．

查看解析
20、已知，如图，在平行四边形ABCD中，AB＝3cm ， BC＝5cm ， AC⊥AB ， △ACD沿AC的方向匀速平移得到△PNM ，速度为1cm/s；同时，点Q从点C出发，沿CB方向匀速移动，速度为1cm/s ，当△PNM停止平移时，点Q也停止移动，如图②，设移动时间为t（s）（0＜t＜4），连接PQ ， MQ ， MC ，解答下列问题：

(1)、当t为何值时，PQ∥MN；

(2)、设△QMC的面积为y（cm2），求y与t之间的函数关系式；

(3)、是否存在某一时刻t ，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由．

查看解析

上一页 76 77 78 79 80 下一页跳转