2025年山东省济南市中考数学模拟试卷（2）

试卷日期：2025-03-27 考试类型：中考模拟

前去【出卷网】下载

一、选择题（每题3分，共30分）

1. 热气球上升5米记为+5，则下降3米应该记为（）

A、3 B、2 C、-2 D、-3

查看试题解析
2. 如图，往一个密封的正方体容器持续注入一些水，注水的过程中，可将容器任意放置，水平面形状不可能是（）

A、三角形 B、正方形 C、六边形 D、七边形

查看试题解析
3. 如果一个正多边形的内角和等于1080°，那么该正多边形的一个外角等于（）

A、30° B、45° C、60° D、72°

查看试题解析
4. 定义：由a ， b构造的二次函数 $y = a x^{2} + (a + b) x + b$ 叫做一次函数 $y = a x + b$ 的“滋生函数”．若一次函数 $y = a x + b$ 的“滋生函数”是 $y = a x^{2} - 3 x + a + 1$ ， t是关于x的方程 $x^{2} + b x + a - b = 0$ 的根，且 $t > 0$ ，则 $t^{3} - 2 t^{2} + 1$ 的值为（）

A、0 B、1 C、 $\sqrt{5} + 1$ D、 $3 - \sqrt{5}$

查看试题解析
5. 在一次包饺子活动中，五位家庭成员包的饺子个数分别为6，12，20，24，30(其中爸爸包了12个).后来爸爸又包了8个，所得5个数据与原数据相比，以下几个统计量中，不变的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
6. 如图，在 $△ A B C$ 中，点 $D$ 在BC边上， $2 ∠ B = ∠ D A C, C E ⊥ A D$ ，若 $A E = D E = 2$ ， $A C = 6$ ，则BC的长为（）

A、10 B、 $5 \sqrt{3}$ C、8 D、 $8 \sqrt{2}$

查看试题解析
7. 定义：如果一元二次方程ax²+bx+c=0（a≠0）满足a+b+c=0，那么我们称这个方程为“和谐”方程；如果一元二次方程ax²+bx+c=0（a≠0）满足a﹣b+c=0那么我们称这个方程为“美好”方程，如果一个一元二次方程既是“和谐”方程又是“美好”方程，则下列结论正确的是（　　）

A、方程有两个相等的实数根 B、方程有一根等于0 C、方程两根之和等于0 D、方程两根之积等于0

查看试题解析
8. 如图， $A B$ 是 $⊙ O$ 的直径， $C D$ 是弦，若 $∠ C D B = 32 °$ ，则 $∠ A B C$ 等于（）

A、68° B、64° C、58° D、32°

查看试题解析
9. 如图，在△ABC中，AB＝AC＝5，BC＝6，D，E分别为线段AB，AC
上一点，且AD＝AE，连接BE、CD交于点G，延长AG交BC于点F．以下四个结论正确的是（）
①BF＝CF； ②若BE⊥AC，则CF＝DF；
③连结EF，若BE⊥AC，则∠DFE＝2∠ABE
④.若BE平分∠ABC，则FG= $\frac{3}{2}$ ；

A、①②③ B、③④ C、①②④ D、①②③④

查看试题解析

二、填空题（每题3分，共15分）

10. 写出一个小于4的无理数.

查看试题解析
11. 某厂生产了1000只灯泡.为了解这1000只灯泡的使用寿命，从中随机抽取了50只灯泡进行检测，获得了它们的使用寿命（单位：小时），数据整理如下：
使用寿命
$x < 1000$
$1000 ⩽ x < 1600$
$1600 ⩽ x < 2200$
$2200 ⩽ x < 2800$
$x ⩾ 2800$
灯泡只数
5
10
12
17
6
根据以上数据，估计这1000只灯泡中使用寿命不小于2200小时的灯泡的数量为只.

查看试题解析
12. 如图，在菱形ABCD中， $∠ A = 6 0^{°}, A B = 4$ ，点 $E$ 为AB中点，将菱形沿FG折叠，使点 $C$ 与点 $E$ 重合，连结EF，~EG，则 $B G =$ ．

查看试题解析
13. 如图，线段 $A B$ 与 $y$ 轴平行，点 $A$ 的坐标为 $(- 1, a)$ ，将线段 $A B$ 沿着 $x$ 轴水平向左平移到线段 $C D$ ，点 $B$ 的对应点 $D$ 的坐标为 $(- 3, a + 6)$ ，反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象同时经过点 $B$ 与点 $C$ ．则 $k$ 的值为．

查看试题解析
14. 如图是王先生家的菜团，图2是该菜谱的示意图，该菜谱可看作矩形，点 $E$ ， $F$ 分别是矩形 $A B C D$ 的边 $C D$ ， $A B$ 的中点，两条平行线 $A K$ ， $C L$ 分别经过菱形 $E G F H$ 的顶点 $H$ ， $G$ 和边 $F G$ ， $E H$ 的中点 $M$ ， $N$ ．已知菱形 $E G F H$ 的面积为6，则阴影部分的面积之和为．

查看试题解析

三、解答题（共9题，共105分）

15. 计算题

(1)、计算： $\sqrt{0.04}$ +cos²45°﹣（﹣2）^﹣¹﹣|﹣ $\frac{1}{2}$ |

(2)、先化简，再求值：（ $\frac{x - y}{x^{2} - 2 x y + y^{2}}$ ﹣ $\frac{x}{x^{2} - 2 x y}$ ）÷ $\frac{y}{x - 2 y}$ ，其中x=2 $\sqrt{2}$ ，y= $\sqrt{2}$ ．

查看试题解析
16. 如图，在 $△ A B C$ 中， $C E ⊥ A B$ 于点 $E$ ，点 $D$ 在 $B C$ 上，连结 $A D$ 交 $C E$ 于点 $F$ ， $B C = 13$ ， $C E = 12$ .

(1)、求 $B E$ 的长；

(2)、若 $∠ A F E = 45^{\circ}, A B = C F$ ，求 $A E$ 的长.

查看试题解析
17. 某小区门口安装了汽车出入道闸．道闸关闭时，如图1，四边形 $A B C D$ 为矩形， $A B$ 长3米， $A D$ 长1米， $A H$ 与水平地面垂直．道闸打开的过程中，边 $A D$ 固定，连杆 $A B$ ， $C D$ 分别绕点 $A$ ， $D$ 转动，且边 $B C$ 始终与边 $A D$ 平行．

(1)、如图2，当道闸打开至 $∠ A D C =45 °$ 时，边 $C D$ 上一点 $P$ 到 $D$ 的距离 $P D$ 为 $\sqrt{2}$ 米， $P$ 到地面的距离 $P E$ 为1.2米，求点 $D$ 到地面的距离 $D H$ 的长．

(2)、一辆轿车过道闸，已知轿车宽1.8米，高1.6米．当道闸打开至 $∠ A D C = 36 °$ 时，轿车能否驶入小区？请说明理由．（参考数据： $\sin 36 ° \approx 0.59$ ， $\cos 36 ° \approx 0.81$ ， $\tan 36 ° \approx 0.73$ ）

查看试题解析
18. 如图， $A B$ 为 $⊙ O$ 的直径， $A C$ 为 $⊙ O$ 的弦． $∠ A C B$ 的平分线交 $⊙ O$ 于点D．

(1)、若 $∠ A D C = 35 °$ ，求 $∠ C A B$ 的度数；

(2)、若 $A B = 6$ ，求 $△ A B D$ 的面积．

查看试题解析
19. 中学生心理健康受到社会的广泛关注，某校开展心理健康教育专题讲座，就学生对心理健康知识的了解程度，采用随机抽样调查的方式，根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．

根据图中信息回答下列问题：

(1)、接受问卷调查的学生共有___________人，条形统计图中m的值为___________，扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为___________；

(2)、若该校共有学生800人，根据上述调查结果，可以估计出该校学生中对心理健康知识“不了解”的总人数为___________人；

(3)、若某班要从对心理健康知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加心理健康知识竞赛，请用列表或画树状图的方法，求恰好抽到2名女生的概率．

查看试题解析
20. “直播带货”已经成为信息社会中商家的一种新型促销手段，2024年是中国农历甲辰龙年，某主播用3000元购进了一批“小金龙”布偶玩具在直播间销售，由于销售火爆，又用9900元购进了第二批这种玩具，所购数量是第一批购进数量的3倍，但每件的进价贵了3元．

(1)、求商场购进第一批“小金龙 $^{^{'}}$ 每件的进价．

(2)、直播间在第二批“小金龙”布偶销售过程中发现，“小金龙”布偶每分钟的销量 $y$ （件）与销售单价 $x$ （元）满足一次函数关系 $y = - 10 x + 410$ ，设每分钟的销售利润为 $w$ 元，求 $w$ 与 $x$ 之间的函数关系式，并求 $w$ 最大值．

查看试题解析
21. 如图，一次函数 $y_{1} = k x + b (k \neq 0)$ 的图象与反比例函数 $y_{2} = \frac{m}{x} (m \neq 0)$ 的图象相交于 $A (1,3) ， B (n, - 1)$ 两点．

(1)、求一次函数和反比例函数的表达式；

(2)、根据图象直接写出 $y_{1} > y_{2}$ 时， $x$ 的取值范围；

(3)、过点 $B$ 作直线 $O B$ ，交反比例函数图象于点 $C$ ，连结 $A C$ ，求 $△ A B C$ 的面积．

查看试题解析
22.

(1)、【情境再现】
如图 $1$ ，在正方形 $A B C D$ 中，点 $E$ 、 $F$ 分别在边 $A B$ 、 $B C$ 上，且 $D E ⊥ A F$ ，求证： $D E = A F$ ．

(2)、【迁移应用】
如图 $2$ ，在矩形 $A B C D$ 中， $A D = k A B (k$ 为常数 $)$ ，点 $E$ 、 $F$ 、 $G$ 、 $H$ 分别在矩形 $A B C D$ 的边上，且 $E G ⊥ F H$ ，求证： $E G = k F H$ ．

(3)、【拓展延伸】
如图 $3$ ，在四边形 $A B C D$ 中， $∠ A B C = ∠ A D C = 90 °$ ， $∠ B C D = 60 °$ ， $C D = 4$ ，点 $E$ 、 $F$ 分别在边 $A B$ 、 $B C$ 上，且 $C E ⊥ D F$ ， $\frac{D F}{C E} = 4 \sqrt{3} - 6$ ，求 $A B$ 的长．

查看试题解析
23. 如图抛物线y＝x²+bx+c（c＜0）与x轴交于A、B两点，（点A在点B的左侧），与y轴交于点C，顶点为D，且OB＝OC＝3，点E为线段BD上的一个动点，EF⊥x轴于F.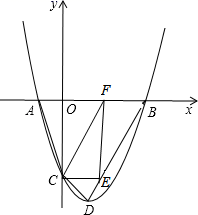

(1)、求抛物线的解析式；

(2)、是否存在点E，使△ECF为直角三角形？若存在，求点E的坐标；不存在，请说明理由；

(3)、连接AC、BC，若点P是抛物线上的一个动点，当P运动到什么位置时，∠PCB＝∠ACO，请直接写出点P的坐标.

查看试题解析

使用寿命	$x < 1000$	$1000 ⩽ x < 1600$	$1600 ⩽ x < 2200$	$2200 ⩽ x < 2800$	$x ⩾ 2800$
灯泡只数	5	10	12	17	6