2016-2017学年四川省乐山市沙湾区沫若中学高一上学期期中数学试卷
试卷日期:2016-12-21 考试类型:期中考试
一、选择题
-
1. 已知U={1,2,3,4},A={1,3,4},B={2,3,4},那么∁U(A∩B)=( )A、{1,2} B、{1,2,3,4} C、∅ D、{∅}2. 如果A={x|x>﹣1},那么下列表示正确的是( )A、0⊆A B、{0}∈A C、∅∈A D、{0}⊆A3. 给出下列四个对应:如图,其构成映射的是( )
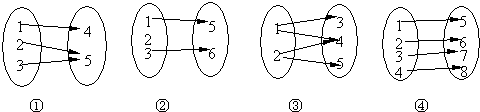 A、只有①② B、只有①④ C、只有①③④ D、只有③④4. 函数f(x)= 的定义域为( )A、[2,3) B、(2,3) C、[2,+∞) D、(﹣∞,3]5. 已知函数f(x)= ,则f(f( ))=( )A、 B、 C、 D、6. 若奇函数f(x)在[3,7]上是增函数,且最小值是1,则它在[﹣7,﹣3]上是( )A、增函数且最小值是﹣1 B、增函数且最大值是﹣1 C、减函数且最大值是﹣1 D、减函数且最小值是﹣17. 函数y=f(x)是R上的偶函数,且在(﹣∞,0]上是增函数,若f(a)≤f(2),则实数a的取值范围是( )A、a≤2 B、a≥﹣2 C、a≤﹣2或 a≥2 D、﹣2≤a≤28. 函数y=ax﹣ (a>0,a≠1)的图象可能是( )A、
A、只有①② B、只有①④ C、只有①③④ D、只有③④4. 函数f(x)= 的定义域为( )A、[2,3) B、(2,3) C、[2,+∞) D、(﹣∞,3]5. 已知函数f(x)= ,则f(f( ))=( )A、 B、 C、 D、6. 若奇函数f(x)在[3,7]上是增函数,且最小值是1,则它在[﹣7,﹣3]上是( )A、增函数且最小值是﹣1 B、增函数且最大值是﹣1 C、减函数且最大值是﹣1 D、减函数且最小值是﹣17. 函数y=f(x)是R上的偶函数,且在(﹣∞,0]上是增函数,若f(a)≤f(2),则实数a的取值范围是( )A、a≤2 B、a≥﹣2 C、a≤﹣2或 a≥2 D、﹣2≤a≤28. 函数y=ax﹣ (a>0,a≠1)的图象可能是( )A、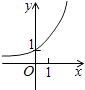 B、
B、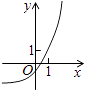 C、
C、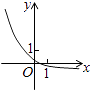 D、
D、 9. 设a=log32,b=log5 ,c=log23,则( )A、a>c>b B、b>c>a C、c>b>a D、c>a>b10. 已知函数f(x)=﹣x2+4x+a,x∈[0,1],若f(x)有最小值﹣2,则f(x)的最大值为( )A、1 B、0 C、﹣1 D、211. 已知奇函数f(x)在(﹣∞,0)上单调递减,且f(2)=0,则不等式xf(x﹣1)>0的解集是( )A、(﹣3,﹣1) B、(﹣3,1)∪(2,+∞) C、(﹣3,0)∪(3,+∞) D、(﹣1,0)∪(1,3)12. 已知函数f(x)=|log4x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m2 , n]上的最大值为2,则m,n的值分别为( )A、 , 2 B、 , 4 C、 , 2 D、 , 4
9. 设a=log32,b=log5 ,c=log23,则( )A、a>c>b B、b>c>a C、c>b>a D、c>a>b10. 已知函数f(x)=﹣x2+4x+a,x∈[0,1],若f(x)有最小值﹣2,则f(x)的最大值为( )A、1 B、0 C、﹣1 D、211. 已知奇函数f(x)在(﹣∞,0)上单调递减,且f(2)=0,则不等式xf(x﹣1)>0的解集是( )A、(﹣3,﹣1) B、(﹣3,1)∪(2,+∞) C、(﹣3,0)∪(3,+∞) D、(﹣1,0)∪(1,3)12. 已知函数f(x)=|log4x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m2 , n]上的最大值为2,则m,n的值分别为( )A、 , 2 B、 , 4 C、 , 2 D、 , 4二、填空题
-
13. 有15人进了家电超市,其中有9人买了电视机,有7人买了电脑,两种均买了的有3人,则这两种均没买的有人.14. 已知函数f(x)=a﹣ ,若f(x)为奇函数,则a= .15. 若3x=4y=36,则 = .16. 下列各式:
(1)已知loga <1,则a> ;
(2)函数y=2x的图象与函数y=2﹣x的图象关于y轴对称;
(3)函数f(x)=lg(mx2+mx+1)的定义域是R,则m的取值范围是0≤m<4;
(4)函数y=ln(﹣x2+x)的递增区间为(﹣∞, ]
正确的有 . (把你认为正确的序号全部写上)
三、解答题
-
17. 计算:(1)、0.25×( )﹣4﹣4÷( ﹣1)0﹣( ) ;(2)、lg25+lg2•lg50+(lg2)2 .18. 已知函数f(x)=x2﹣2|x|﹣1.(1)、证明函数f(x)是偶函数;(2)、在如图所示的平面直角坐标系中作出函数f(x)的图象.并根据图象写出函数f(x)的单调区间;
 (3)、求函数f(x)当x∈[﹣2,4]时的最大值与最小值.19. 为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.57元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.(1)、设月用电x度时,应交电费y元,写出y关于x的函数关系式;(2)、小明家第一季度缴纳电费情况如下:问小明家第一季度共用电多少度?
(3)、求函数f(x)当x∈[﹣2,4]时的最大值与最小值.19. 为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.57元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.(1)、设月用电x度时,应交电费y元,写出y关于x的函数关系式;(2)、小明家第一季度缴纳电费情况如下:问小明家第一季度共用电多少度?月份
一月
二月
三月
合计
交费金额
76元
63元
45.6元
184.6元