2016-2017学年广西贵港市港南区九年级上学期期中数学试卷
试卷日期：2016-12-17 考试类型：期中考试
一、选择题
-
1. 方程（x﹣2）（x+3）=0的解是（ ）A、x=2 B、x=﹣3 C、x1=﹣2，x2=3 D、x1=2，x2=﹣32. 抛物线y=2（x﹣3）2+1的顶点坐标是（ ）A、（3，1） B、（4，﹣1） C、（﹣3，1） D、（﹣3，﹣1）3. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、等边三角形
B、平行四边形
C、正方形 
D、正五边形
4. 一元二次方程2x2﹣5x+1=0的根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定5. 若n（n≠0）是关于x的方程x2+mx+2n=0的根，则m+n的值为（ ）A、1 B、2 C、﹣1 D、﹣26. 下列说法正确的是（ ）A、长度相等的两条弧是等弧 B、平分弦的直径垂直于弦 C、直径是同一个圆中最长的弦 D、过三点能确定一个圆7. 若点P（m，﹣m+3）关于原点的对称点Q在第三象限，那么m的取值范围是（ ）A、0＜m＜3 B、m＜0 C、m＞0 D、m≥08. 某超市一月份的营业额为36万元，三月份的营业额为48万元，设每月的平均增长率为x，则可列方程为（ ）A、48（1﹣x）2=36 B、48（1+x）2=36 C、36（1﹣x）2=48 D、36（1+x）2=489. 若两个连续整数的积是56，则它们的和为（ ）A、11 B、15 C、﹣15 D、±1510. 如图，圆弧形桥拱的跨度AB=12米，拱高CD=4米，则拱桥的半径为（ ）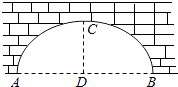
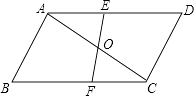
A、6.5米 B、9米 C、13米 D、15米11. 如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD等于（ ）
A、16° B、32° C、58° D、64°12. 如图所示，已知△ABC与△CDA关于点O对称，过O任作直线EF分别交AD，BC于点E，F，下面的结论：①点E和点F，点B和点D是关于中心O对称点；
②直线BD必经过点O；
③四边形DEOC与四边形BFOA的面积必相等；
④△AOE与△COF成中心对称．
其中正确的个数为（ ）
A、1 B、2 C、3 D、4二、填空题
-
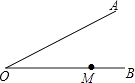
13. 把方程（2x+1）2﹣x=（x+1）（x﹣1）化成一般形式是 ．14. 若x=﹣2是关于x的一元二次方程x2﹣mx+8=0的一个解，则m的值是15. 若函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是 ．16. 正三角形中心旋转度的整倍数之后能和自己重合．17. 如图，∠AOB=30°，OM=6，那么以M为圆心，4为半径的圆与直OA的位置关系是
18. 如图①，在△AOB中，∠AOB=90°，OA=3，OB=4．将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转，分别得到图②、图③、…，则旋转得到的图⑩的直角顶点的坐标为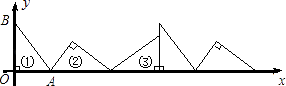
三、解答题
-
19. 解答(1)、7x（5x+2）=6（5x+2）(2)、关于x的一元二次方程x2+3x+m﹣1=0有两个实数根，求m的取值范围．20. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
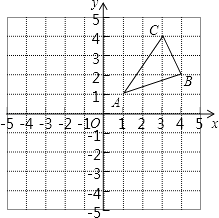(1)、①请画出△ABC向左平移5个单位长度后得到的△A1B1C1；②请画出△ABC关于原点对称的△A2B2C2；
(2)、在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标．21.如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB，BC各为多少米？
22. 如图，PA，PB是⊙O的切线，A，B为切点，∠OAB=30度．
(1)、求∠APB的度数；(2)、当OA=3时，求AP的长．23. 某商场在销售中发现：某名牌衬衣平均每天可售出20件，每件衬衣盈利40元．为了迎接元旦节，扩大销售量，减少库存，商场决定采取适当的降价措施，经市场调查发现，如果每件衬衣降价1元，商场平均每天可多售出2件．要想平均每天盈利1200元，每件衬衣应降价多少元？24. 如图，在Rt△ABC中，∠ACB=90°，∠B=30°，将△ABC绕点C按顺时针方向旋转n度后，得到△DEC，点D刚好落在AB边上．
(1)、求n的值；(2)、若F是DE的中点，判断四边形ACFD的形状，并说明理由．25. 已知抛物线C1：y=ax2+4ax+4a+b（a≠0，b＞0）的顶点为M，经过原点O且与x轴另一交点为A．(1)、求点A的坐标；(2)、若△AMO为等腰直角三角形，求抛物线C1的解析式；(3)、现将抛物线C1绕着点P（m，0）旋转180°后得到抛物线C2 ， 若抛物线C2的顶点为N，当b=1，且顶点N在抛物线C1上时，求m的值．26.如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．（提示：正方形的四条边都相等，四个角都是直角）
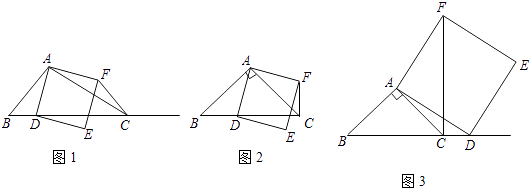(1)、如果AB=AC，∠BAC=90°，①当点D在线段BC上时（与点B不重合），如图2，线段CF，BD所在直线的位置关系为 ， 线段CF，BD的数量关系为；
②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；
(2)、如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足条件时，CF⊥BC（点C，F不重合），不用说明理由．