2017-2018学年北师大版数学八年级下册同步训练：6.2.2 平行四边形的判定 ——用对角线的关系判定平行四边形
试卷日期：2018-03-19 考试类型：同步测试
一、知识点1由对角线相互关系判定平行四边形
-
1.
如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件（只添一个即可），使四边形ABCD是平行四边形
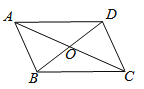2. 下列说法错误的是（ ）A、对角线互相平分的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、一组对边相等，另一组对边平行的四边形是平行四边形3. 如图，在▱ABCD中，对角线AC，BD相交于点O，E，F是对角线AC上的两点，当点E，F满足下列哪个条件时，四边形DEBF不一定是平行四边形（ ）
A、OE=OF B、DF=BE C、AE=CF D、∠AEB=∠CFD4. 如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD=90°，BC=4，BE=ED=3，AC=10，则四边形ABCD的面积为（ ）
A、6 B、12 C、20 D、245. 如图，在▱ABCD中，点E，F在AC上，且AE=CF.求证：四边形BEDF是平行四边形.
二、知识点2平行四边形判定方法的综合应用
-
6. 在四边形ABCD中，AC交BD于点O，且AB∥CD，给出以下四种说法：
①如果再加上条件“BC=AD”，那么四边形ABCD一定是平行四边形；
②如果再加上条件“∠BAD=∠BCD”，那么四边形ABCD一定是平行四边形；
③如果再加上条件“AO=OC”，那么四边形ABCD一定是平行四边形；
④如果再加上条件“∠DBA=∠CAB”，那么四边形ABCD一定是平行四边形.
其中正确的说法是（ ）
A、①② B、①③④ C、②③ D、②③④7. 下列命题中，真命题有（ ）①对角线互相平分的四边形是平行四边形；
②两组对角分别相等的四边形是平行四边形；
③一组对边平行，另一组对边相等的四边形是平行四边形.
A、3个 B、2个 C、1个 D、0个8. 在四边形ABCD中，对角线AC，BD相交于点O，给出下列四组条件：①AB∥CD，AD∥BC；
②AB=CD，AD=BC；
③AO=CO，BO=DO；
④AB∥CD，AD=BC.
其中一定能判定这个四边形是平行四边形的条件有（ ）
A、1组 B、2组 C、3组 D、4组9. 如图，在▱ABCD中，对角线AC，BD相交于O，E，F是对角线上的两点，给出下列四个条件：①OE=OF；
②DE=BF；③∠ADE=∠CBF；④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有（ ）
A、0个 B、1个 C、2个 D、3个10. 如图，▱ABCD的对角线相交于点O，直线EF经过点O，分别与AB，CD的延长线交于点E，F.求证：四边形AECF是平行四边形.
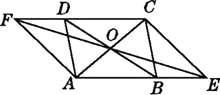11. 如图，已知点E，C在线段BF上，BE=EC=CF，AB∥DE，∠ACB=∠F.
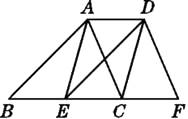(1)、求证：△ABC≌△DEF；(2)、试判断：四边形AECD的形状，并说明理由.12. 如图，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D'处，直线l交CD边于点E，连接BE.
(1)、求证：四边形BCED'是平行四边形；(2)、若BE平分∠ABC，求证：AB2=AE2+BE2.13. 在△ABC中，AB=AC，点D在边BC所在的直线上，过点D作DE∥AC交直线AB于点E，DF∥AB交直线AC于点F.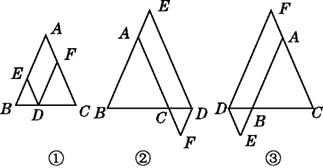
(1)、当点D在边BC上时，如图①，求证：DE+DF=AC.(2)、当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③.请分别写出图②、图③中DE，DF，AC之间的数量关系，不需要证明.
(3)、若AC=6，DE=4，则DF=.