2017-2018学年北师大版数学八年级下册同步训练：6.2.1 平行四边形的判定——用边的关系判定平行四边形
试卷日期：2018-03-19 考试类型：同步测试
一、知识点1由两组对边关系判定平行四边形
-
1. 要判定四边形是平行四边形,若从边的位置关系的角度去判定,需两组对边分别.若从边的数量关系的角度去判定,需两组对边分别.
2. 在四边形ABCD中，AD∥BC，当满足条件（ ）时，四边形ABCD是平行四边形.
A、∠A+∠C=180° B、∠B+∠D=180° C、∠A+∠B=180° D、∠A+∠D=180°3. A，B，C是平面内不在同一条直线上的三点，D是平面内任意一点，若A，B，C，D四点恰能构成一个平行四边形，则在平面内符合这样条件的点D有（ ）
A、1个 B、2个 C、3个 D、4个4. 下列图形中，一定可以拼成平行四边形的是（ ）
A、两个等腰三角形 B、两个直角三角形 C、两个锐角三角形 D、两个全等三角形5. 已知直角坐标系内有四个点O(0，0)，A(3，0)，B(1，1)，C(x，1)，若以O，A，B，C为顶点的四边形是平行四边形，则x=.6. 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图所示的四边形ABCD，并写出了如下不完整的已知和求证.已知：如图，在四边形ABCD中，BC=AD，
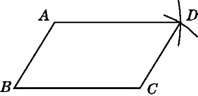
AB=__①___.
求证：四边形ABCD是___②___四边形.
(1)、在方框中填空，以补全已知和求证；①；②.
(2)、按嘉淇的想法写出证明.
(3)、用文字叙述所证命题的逆命题为
二、知识点2由一组对边关系判定平行四边形
-
7. 一组对边且的四边形是平行四边形.
8. 在四边形ABCD中，AD=BC，若四边形ABCD是平行四边形，则还应满足（ ）
A、∠A+∠C=180° B、∠B+∠D=180° C、∠A+∠B=180° D、∠A+∠D=180°9. 不能判定四边形ABCD为平行四边形的条件是（ ）
A、AB=CD，AD=BC B、AB=CD，AB∥CD C、AB=CD，AD∥BC D、AD=BC，AD∥BC10. 如图，在▱ABCD中，点E，F分别在AD，BC上，若要使四边形AFCE是平行四边形，可以添加的条件是（ ）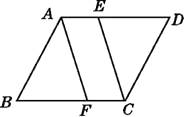
①AF=CF；②AE=CE；③BF=DE；④AF∥CE.
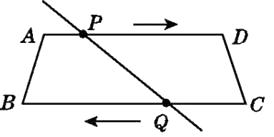
A、①或② B、②或③ C、③或④ D、①或③11. 如图，在▱ABCD中，E，F分别是AB，CD的中点，连接DE，EF，BF，则图中平行四边形共有（ ）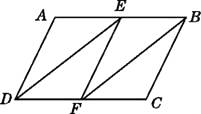
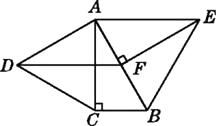
A、2个 B、4个 C、6个 D、3个12. 如图，在四边形ABCD中，AD∥BC，且AD>BC，BC=6 cm，动点P，Q分别从A，C同时出发，P以1 cm/s的速度由A向D运动，Q以2 cm/s的速度由C向B运动(Q运动到B时两点同时停止运动)，则后四边形ABQP为平行四边形.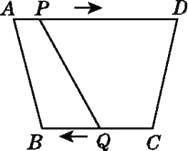
13. 如图，已知BD是△ABC的角平分线，点E，F分别在边AB，BC上，ED∥BC，EF∥AC.求证：BE=CF.
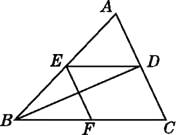14. 如图，在▱ABCD中，E，F分别为边AD，BC的中点，对角线AC分别交BE，DF于点G，H.求证：AG=CH.
