广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
试卷日期：2018-03-06 考试类型：期末考试
一、选择题
-
1. 下列图形中既是中心对称图形又是轴对称图形的是（ ）。A、
B、
C、
D、
2. 一个不透明的袋中有2个红球，3个白球，这些球除颜色外其余都相同，从口袋中随机摸出一个球，这个球是白球的概率是（ ）
A、 B、 C、 D、3. 二次函数y=(x-5)2+7的最小值是（ ）
A、5 B、-7 C、-5 D、74. 下列关于x的一元二次方程有实数根的是（ ）A、x2+2=0 B、2x2+x+1=0 C、x2-x+3=0 D、x2-2x-1=05. P(-3，4)关于原点对称的点的坐标是（ ）
A、(3，4) B、(3，-4) C、(-3，-4) D、(4，一3)6. 如图，∠A是⊙O的圆周角，∠A=40。 ， 则∠BOC=（ ）
A、20。 B、40。 C、60。 D、80。7. 在平面直角坐标系中，⊙O的半径为5，圆心在原点0，则P(-3，4)与⊙0的位置关系是（ ）
A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定8. 如图，⊙O的直径CD垂直弦AB于点E，且CE=2，OB=4，则AB的长为（ ）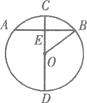
A、2 B、4 C、6 D、49. 三角形的两边长分别为3和6，第三边的长是方程x2-6x+8=0的一个根，则这个三角形的周长是（ ）
A、11或13 B、13或15 C、13 D、1110. 在同一坐标系中，一次函数y=mx+n2与二次函数y=x2+m的图象可能是（ ）
A、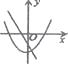
B、
C、
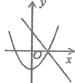D、
二、填空题
-
11. 一元二次方程x2-4=0的解是 ．
12. 圆内接四边形ABCD中，已知∠A=120。 ， 则∠C= ．
13. 函数y=x2+4x+4与坐标轴的交点坐标分别是 ．
14. 如图，在△ABC中，∠BAC=60。 ， 将△ABC绕着点A顺时针旋转40。后得到△ADE。则∠BAE的度数为 ．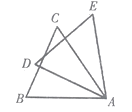
15. 如图，过⊙O上一点C作⊙O的切线，交OD的直径AB的延长线于点D．若∠D=40。 ， 则∠A的度数为 ．
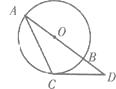16. 一块等边三角形木板，边长为1，现将木板沿水平线翻滚，如图所示，若翻滚了20次．则B点所经过的路径长度为 ．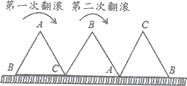
三、解答题
-
17. 解方程：2x(x+4)=118. 如图，点A的坐标为(3，3)，点B的坐标为(4，0)。点C的坐标为(0，-1)．
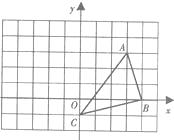(1)、请在直角坐标系中画出△ABC绕着点C逆时针旋转90°后的△A’B’C’(2)、直接写出：点A’的坐标( ， )，点B’的坐标( ， )．19. 如图，在Rt△OAB中，∠OAB=90。 ， OA=AB=6，将△OAB绕点O沿逆时针方向旋转90。得到△OA1B1 ．
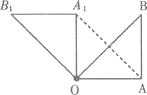(1)、求线段OA1的长及∠AOB1；
(2)、连接AA1 ， 求四边形OAA1B1的面积．
四、解答题
-
20. 已知关于x的方程x2+2x+a-2=0一个根为1 。
(1)、求a的值及方程的另一根．(2)、以原点为圆心，｜a｜为半径作圆，判断点P(1，1)与该圆的位置关系。
21. 不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同)，其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为 ．
(1)、试求袋中蓝球的个数；
(2)、第一次任意摸一个球(不放回)，第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率．22. 现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，韶关市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．(1)、求该快递公司投递总件数的月平均增长率；
(2)、今年6月份的快递投递量是多少?
五、解答题
-
23. 将一条长度为40cm的绳子剪成两段，并以每一段绳子的长度为周长围成一个正方形．(1)、要使这两个正方形的面积之和等于58cm2 ， 那么这段绳子剪成两段后的长度分别是多少?
(2)、两个正方形的面积之和可以是40吗?说明理由．
(3)、求两个正方形的面积之和的最小值，此时两个正方形的边长分别是多少?24. 如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．以AB上某一点O为圆心作⊙O。使⊙O经过点A和点D．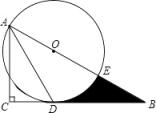
(1)、判断直线BC与⊙O的位置关系，并说明理由；(2)、若AC=3，∠B=30°．求⊙O的半径；(3)、在(2)的条件下，设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的图形面积．
25. 如图，抛物线y=-x2+5x+n经过点A(1，0)，与y轴交于点B．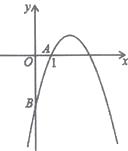
(1)、求抛物线的解析式；(2)、直接写出将抛物线y=-x2+5x+n沿着坐标轴方向经过怎样的一次平移，可以使它经过原点．(3)、P是y轴上一点，且△PAB是以AB为腰的等腰三角形，试求P点坐标．