2017-2018学年人教版数学八年级下册同步训练: 18.2.3《正方形》
试卷日期:2018-03-01 考试类型:同步测试
一、选择题
-
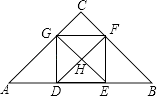
1. 如图,△ABC是一个等腰直角三角形,DEFG是其内接正方形,H是正方形的对角线交点;那么,由图中的线段所构成的三角形中相互全等的三角形的对数为( )
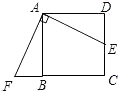
 A、12 B、13 C、26 D、302. 如图所示,E.F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )
A、12 B、13 C、26 D、302. 如图所示,E.F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )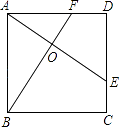 A、1个 B、2个 C、3个 D、4个3. 如图,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个3. 如图,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有( )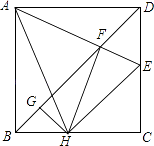 A、①②③ B、①②④ C、①③④ D、①②③④4. 一个围棋盘由18×18个边长为1的正方形小方格组成,一块边长为1.5的正方形卡片放在棋盘上,被这块卡片覆盖了一部分或全部的小方格共有n个,则n的最大值是( )A、4 B、6 C、10 D、125. 如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )
A、①②③ B、①②④ C、①③④ D、①②③④4. 一个围棋盘由18×18个边长为1的正方形小方格组成,一块边长为1.5的正方形卡片放在棋盘上,被这块卡片覆盖了一部分或全部的小方格共有n个,则n的最大值是( )A、4 B、6 C、10 D、125. 如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )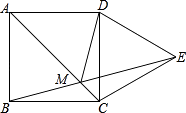 A、75° B、60° C、54° D、67.5°6. 在平面直角坐标系中,称横.纵坐标均为整数的点为整点,如下图所示的正方形内(包括边界)整点的个数是( )
A、75° B、60° C、54° D、67.5°6. 在平面直角坐标系中,称横.纵坐标均为整数的点为整点,如下图所示的正方形内(包括边界)整点的个数是( )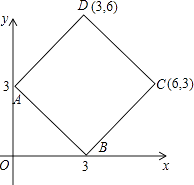 A、13 B、21 C、17 D、257. 在同一平面上,正方形ABCD的四个顶点到直线l的距离只取四个值,其中一个值是另一个值的3倍,这样的直线l可以有( )A、4条 B、8条 C、12条 D、16条8. 如图,正方形ABCD的边长为1,E为AD中点,P为CE中点,F为BP中点,则F到BD的距离等于( )
A、13 B、21 C、17 D、257. 在同一平面上,正方形ABCD的四个顶点到直线l的距离只取四个值,其中一个值是另一个值的3倍,这样的直线l可以有( )A、4条 B、8条 C、12条 D、16条8. 如图,正方形ABCD的边长为1,E为AD中点,P为CE中点,F为BP中点,则F到BD的距离等于( )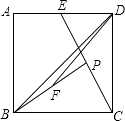 A、 B、 C、 D、9. 搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2 , 则被分隔开的△CON的面积为( )
A、 B、 C、 D、9. 搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2 , 则被分隔开的△CON的面积为( ) A、96cm2 B、48cm2 C、24cm2 D、以上都不对10. 如图,正方形ABCD的对角线AC与BD相交于O点,在BD上截取BE=BC,连接CE,点P是CE上任意一点,PM⊥BD于M,PN⊥BC于N,若正方形ABCD的边长为1,则PM+PN=( )
A、96cm2 B、48cm2 C、24cm2 D、以上都不对10. 如图,正方形ABCD的对角线AC与BD相交于O点,在BD上截取BE=BC,连接CE,点P是CE上任意一点,PM⊥BD于M,PN⊥BC于N,若正方形ABCD的边长为1,则PM+PN=( )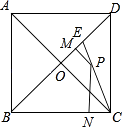 A、1 B、 C、 D、1+11. 顶点为A(6,6),B(-4,3),C(-1,-7),D(9,-4)的正方形在第一象限的面积是( )A、25 B、36 C、49 D、3012. ABCD是边长为1的正方形,△BPC是等边三角形,则△BPD的面积为( )
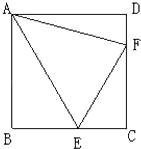
A、1 B、 C、 D、1+11. 顶点为A(6,6),B(-4,3),C(-1,-7),D(9,-4)的正方形在第一象限的面积是( )A、25 B、36 C、49 D、3012. ABCD是边长为1的正方形,△BPC是等边三角形,则△BPD的面积为( ) A、 B、 C、 D、13. 如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为( )
A、 B、 C、 D、13. 如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为( ) A、4 B、2 C、2 D、214. 如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=( )
A、4 B、2 C、2 D、214. 如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=( )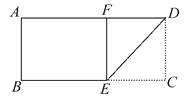 A、4cm B、6cm C、8cm D、10cm15. 如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的周长为( )
A、4cm B、6cm C、8cm D、10cm15. 如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的周长为( )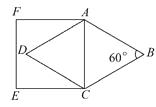
A、14 B、15 C、16 D、17二、填空题
-
16. 如图所示,将五个边长都为1cm的正方形按如图所示摆放,其中点A、B、C、D分别是正方形对角线的交点、如果有n个这样大小的正方形这样摆放,则阴影面积的总和是cm2 .
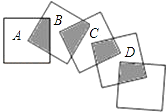 17. 如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为 .
17. 如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为 .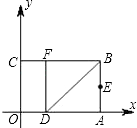 18. 如图,边长为a的正方形ABCD和边长为b的正方形BEFG排放在一起,O1和O2分别是两个正方形的中心,则阴影部分的面积为 , 线段O1O2的长为 .
18. 如图,边长为a的正方形ABCD和边长为b的正方形BEFG排放在一起,O1和O2分别是两个正方形的中心,则阴影部分的面积为 , 线段O1O2的长为 .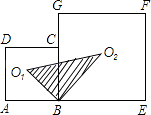 19. 已知正方形ABCD在直角坐标系内,点A(0,1),点B(0,0),则点C,D坐标分别为和 . (只写一组)
19. 已知正方形ABCD在直角坐标系内,点A(0,1),点B(0,0),则点C,D坐标分别为和 . (只写一组)
20. 如图,在一个正方形被分成三十六个面积均为1的小正方形,点A与点B在两个格点上.在格点上存在点C,使△ABC的面积为2,则这样的点C有个.
三、解答题
-
21. 如图,在正方形ABCD中,对角线AC与BD相交于点O,AF平分∠BAC,交BD于点F.
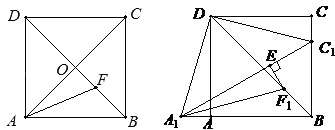 (1)、求证: ;(2)、点A1、点C1分别同时从A、C两点出发,以相同的速度运动相同的时间后同时停止,如图,A1F1平分∠BA1C1 , 交BD于点F1 , 过点F1作F1E⊥A1C1 , 垂足为E,请猜想EF1 , AB与 三者之间的数量关系,并证明你的猜想;(3)、在(2)的条件下,当A1E1=6,C1E1=4时,求BD的长22. 已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF.求证:DE=BF.
(1)、求证: ;(2)、点A1、点C1分别同时从A、C两点出发,以相同的速度运动相同的时间后同时停止,如图,A1F1平分∠BA1C1 , 交BD于点F1 , 过点F1作F1E⊥A1C1 , 垂足为E,请猜想EF1 , AB与 三者之间的数量关系,并证明你的猜想;(3)、在(2)的条件下,当A1E1=6,C1E1=4时,求BD的长22. 已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF.求证:DE=BF.