高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
试卷日期:2018-02-27 考试类型:同步测试
一、选择题
-
1. 在区间 内任取一点,则此点所对应的实数大于1的概率为( )
A、 B、 C、 D、2. 在区间 上随机取一个实数 ,使得 的概率为( )A、 B、 C、 D、3. 如图,在矩形区域 的 两点处各有一个通信基站,假设其信号的覆盖范围分别是扇形区域 和扇形区域 (该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是( )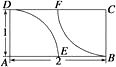 A、 B、 C、 D、4. 如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )
A、 B、 C、 D、4. 如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( ) A、 B、 C、 D、5. 设不等式组 表示的平面区域为
A、 B、 C、 D、5. 设不等式组 表示的平面区域为 ,在区域
,在区域  内随机取一个点,则此点到坐标原点的距离小于
内随机取一个点,则此点到坐标原点的距离小于 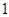 的概率是( ) A、 B、 C、 D、6. 如图,在圆心角为直角的扇形 中,分别以 为直径作两个半圆,在扇形 内随机取一点,则此点取自阴影部分的概率是( )
的概率是( ) A、 B、 C、 D、6. 如图,在圆心角为直角的扇形 中,分别以 为直径作两个半圆,在扇形 内随机取一点,则此点取自阴影部分的概率是( )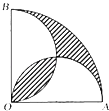 A、 B、 C、 D、7. 依次连接正六边形各边的中点,得到一个小正六边形,再依次连接这个小正六边形各边的中点,得到一个更小的正六边形,往原正六边形内随机撒一粒种子,则种子落在最小的正六边形内的概率为( )A、 B、 C、 D、
A、 B、 C、 D、7. 依次连接正六边形各边的中点,得到一个小正六边形,再依次连接这个小正六边形各边的中点,得到一个更小的正六边形,往原正六边形内随机撒一粒种子,则种子落在最小的正六边形内的概率为( )A、 B、 C、 D、二、单选题
-
8. 有下列四个游戏盘,将它们水平放稳后,向上面扔一颗小玻璃球,若小球落在阴影部分,则可中奖,小明要想增加中奖机会,应选择的游戏盘是( )
A、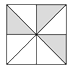 B、
B、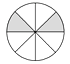 C、
C、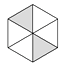 D、
D、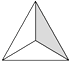
三、填空题
-
9. 如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1 000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为400颗,以此实验数据为依据可以估计出该不规则图形的面积为平方米.(用分数作答)
 10. 假设你家订了一份牛奶,送奶人在早上6:00--7:00之间随机地把牛奶送到你家,而你在早上6:30--7:30之间随机地离家上学,则你在离开家前能收到牛奶的概率是.11. 把半径为2的圆分成相等的四段弧,再将四段弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为 .
10. 假设你家订了一份牛奶,送奶人在早上6:00--7:00之间随机地把牛奶送到你家,而你在早上6:30--7:30之间随机地离家上学,则你在离开家前能收到牛奶的概率是.11. 把半径为2的圆分成相等的四段弧,再将四段弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为 .
四、解答题
-
12. 已知集合 , ,设 ,在集合M内随机取出一个元素 .(1)、求以 为坐标的点落在圆 内的概率;(2)、求以 为坐标的点到直线 的距离不大于 的概率.
-