高中数学人教新课标A版必修2 第一章空间几何体 1.3.2球的体积和表面积

试卷日期：2018-02-27 考试类型：同步测试

前去【出卷网】下载

一、选择题

1. 将直径为2的半圆绕直径所在的直线旋转半周而形成的曲面所围成的几何体的表面积为（　　）

A、2π B、3π C、4π D、6π

查看试题解析
2. 正方体的内切球和外接球的体积之比为（）

A、1∶ $\sqrt{3}$ B、1∶3 C、1∶9 D、1∶3 $\sqrt{3}$

查看试题解析
3. 如果三个球的半径之比是1∶2∶3，那么最大球的表面积是其余两个球的表面积之和的（）

A、 $\frac{5}{9}$ 倍 B、 $\frac{9}{5}$ 倍 C、2倍 D、3倍

查看试题解析
4. 若两球的体积之和是12π，经过两球球心的截面圆周长之和为6π，则两球的半径之差为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 把球的表面积扩大到原来的2倍，那么体积扩大到原来的（）

A、2倍 B、2 $\sqrt{2}$ 倍 C、 $\sqrt{2}$ 倍 D、 $\sqrt[3]{2}$ 倍

查看试题解析
6. 已知四棱锥 $S - A B C D$ 的所有顶点都在同一球面上，底面 $A B C D$ 是正方形且和球心 $O$ 在同一平面内，若此四棱锥的最大体积为 $18$ ，则球 $O$ 的表面积等于（）

A、 $18 π$ B、 $36 π$ C、 $54 π$ D、 $72 π$

查看试题解析
7. 已知S，A，B，C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA=AB=1，BC= $\sqrt{2}$ ，则球O的表面积等于（　　）

A、4π B、3π C、2π D、π

查看试题解析
8. 已知点 $A, B, C, D$ 在同一个球面上， $A B = 3, B C = 4, A C = 5$ ，若四面体 $A B C D$ 体积的最大值为 $10$ ，则这个球的表面积是（）

A、 $\frac{25 π}{4}$ B、 $\frac{125 π}{4}$ C、 $\frac{225 π}{16}$ D、 $\frac{625 π}{16}$

查看试题解析

二、填空题

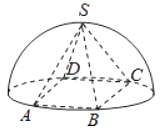
9. 湖面上漂着一个小球，湖水结冰后将球取出，冰面上留下一个直径为12 cm，深为2 cm的空穴，则该球的表面积为cm².

查看试题解析
10. 如图，半球内有一内接正四棱锥 $S - A B C D$ ，该四棱锥的体积为 $\frac{4 \sqrt{2}}{3}$ ，则该半球的表面积为．

查看试题解析
11. 已知正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 底面边长为 $2 \sqrt{3}$ ，高为 $3$ ，圆 $O$ 是等边三角形 $A B C$ 的内切圆，点 $P$ 是圆 $O$ 上任意一点，则三棱锥 $P - A_{1} B_{1} C_{1}$ 的外接球的表面积为．

查看试题解析

三、解答题

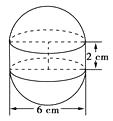
12. 如图，某种水箱用的“浮球”，是由两个半球和一个圆柱筒组成的．已知半球的直径是6 cm，圆柱筒高为2 cm.

(1)、这种“浮球”的体积是多少cm³（结果精确到0.1）?

(2)、要在2 500个这样的“浮球”表面涂一层胶，如果每平方米需要涂胶100克，那么共需胶多少克？

查看试题解析
13. 有三个球，第一个球内切于正方体，第二个球与这个正方体各条棱相切，第三个球过这个正方体的各个顶点，求这三个球的表面积之比．

查看试题解析
14. 如图所示，一个圆锥形的空杯子上放着一个直径为8cm的半球形的冰淇淋，请你设计一种这样的圆锥形杯子（杯口直径等于半球形的冰淇淋的直径，杯子壁厚忽略不计），使冰淇淋融化后不会溢出杯子，怎样设计最省材料？

查看试题解析

高中数学人教新课标A版必修2 第一章 空间几何体 1.3.2球的体积和表面积

一、选择题

二、填空题

三、解答题

高中数学人教新课标A版必修2 第一章空间几何体 1.3.2球的体积和表面积