高中数学人教新课标A版必修2 第四章 圆与方程 4.2.3直线与圆的方程的应用
试卷日期:2018-02-27 考试类型:同步测试
一、选择题
-
1. 圆 ,则经过点 的切线方程为( )A、 B、 C、 D、
-
2. 已知圆的方程为x2+y2-6x-8y=0.设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )A、 B、 C、 D、
-
3. 直线
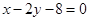 与圆
与圆 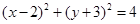 交于
交于 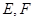 两点,则
两点,则 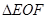 ( 是原点)的面积为( ) A、
( 是原点)的面积为( ) A、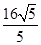 B、
C、
B、
C、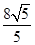 D、
D、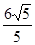
-
4. 若直线 被圆 所截得的弦长为 ,则实数 的值为( )A、 或 B、1或3 C、 或6 D、0或4
-
5. 已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( )A、相切 B、相交 C、相离 D、不确定
-
6. 从圆 外一点 向这个圆作两条切线,则两切线夹角的余弦值为( )A、 B、 C、 D、0
二、单选题
-
7. 半径长为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程为( )A、(x-4)2+(y-6)2=6 B、(x±4)2+(y-6)2=6 C、(x-4)2+(y-6)2=36 D、(x±4)2+(y-6)2=36
-
8. 已知圆 的弦过点 ,当弦长最短时,该弦所在直线方程为( )A、 B、 C、 D、
三、填空题
-
9. 若点 为圆 的弦 的中点,则弦 所在直线的方程为.
-
10. 已知圆 ,直线 与 的交点为 点,过点 向圆 作两条切线 ,分别与圆相切于 两点,则 .
-
11. 已知圆 与直线 相交于 、 两点,则当 的面积最大时,实数 的值为 .
