2017-2018学年华师大版中考数学模拟试卷
试卷日期:2018-02-25 考试类型:中考模拟
一、单选题
-
1. 的相反数是( )A、﹣ B、3 C、﹣3 D、2. 下列LOGO标志中,是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 用小数表示3.56×10﹣7为( )A、0.000000356 B、0.0000000356 C、0.00000000356 D、0.0000000003564. 不等式组 的解集在数轴上表示正确的是( )A、
3. 用小数表示3.56×10﹣7为( )A、0.000000356 B、0.0000000356 C、0.00000000356 D、0.0000000003564. 不等式组 的解集在数轴上表示正确的是( )A、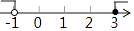 B、
B、 C、
C、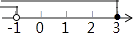 D、
D、 5. 如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
5. 如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )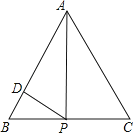 A、
A、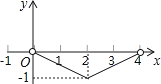 B、
B、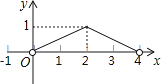 C、
C、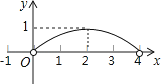 D、
D、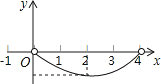 6. 如图,正比例函数y1=k1x的图象与反比例函数y2= 的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
6. 如图,正比例函数y1=k1x的图象与反比例函数y2= 的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )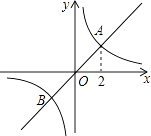 A、x<﹣2或x>2 B、x<﹣2或0<x<2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>27. 把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=32°,则下列结论错误的有( )
A、x<﹣2或x>2 B、x<﹣2或0<x<2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>27. 把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=32°,则下列结论错误的有( )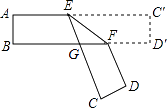 A、∠C′EF=32° B、∠AEC=148° C、∠BGE=64° D、∠BFD=116°8. 如图,已知AB是⊙O的直径,AD切⊙O于点A, .则下列结论中不一定正确的是( )
A、∠C′EF=32° B、∠AEC=148° C、∠BGE=64° D、∠BFD=116°8. 如图,已知AB是⊙O的直径,AD切⊙O于点A, .则下列结论中不一定正确的是( )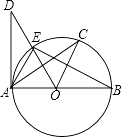 A、BA⊥DA B、OC∥AE C、∠COE=2∠CAE D、OD⊥AC
A、BA⊥DA B、OC∥AE C、∠COE=2∠CAE D、OD⊥AC二、填空题
-
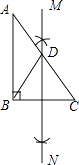
9. 如果 的平方根是±3,则 = .10. 如图,在Rt△ABC中,∠B=90°,按如下步骤作图:
①分别以点B、C为圆心,大于 AB的长为半径作弧,两弧相交于点M和N;
②作直线MN交AC于点D,
③连接BD,
若AC=8,则BD的长为 .
 11. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .
11. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .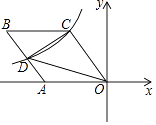 12. 从1、﹣1、0三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率是 .13. 若关于x的分式方程 =2的解为负数,则k的取值范围为 .14. 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作
12. 从1、﹣1、0三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率是 .13. 若关于x的分式方程 =2的解为负数,则k的取值范围为 .14. 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作 交
交  于点C,若OA=2,则阴影部分的面积为 .
于点C,若OA=2,则阴影部分的面积为 . 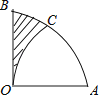 15. 如图,沿矩形ABCD的对角线折叠,先折出折痕AC,再折叠AB,使AB落在对角线AC上,折痕AE,若AD=8,AB=6.则BE= .
15. 如图,沿矩形ABCD的对角线折叠,先折出折痕AC,再折叠AB,使AB落在对角线AC上,折痕AE,若AD=8,AB=6.则BE= .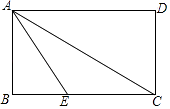
三、解答题
-
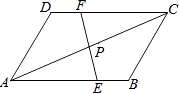
16. 化简分式( ﹣ )÷ ,并从﹣1≤x≤3中选一个你认为合适的整数x代入求值.17. 如图,平行四边形ABCD中,点E、F分别在AB、CD上,且BE=DF,EF与AC相交于点P,求证:PA=PC.
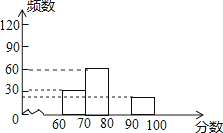
 18. “安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:
18. “安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:分段数
频数
频率
60≤x<70
30
0.15
70≤x<80
60
n
80≤x<90
90≤x<100
20
0.1
合计
m
1
请根据以上图表提供的信息,解答下列问题:
(1)表中m的值为 , n的值为 ;
(2)补全频数分布直方图;
(3)测试成绩的中位数在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约为多少人?
 19. 如图,在△ABC中,AB=AC,以AC为直径的半圆O交BC于点E,DE⊥AB,垂足为D.
19. 如图,在△ABC中,AB=AC,以AC为直径的半圆O交BC于点E,DE⊥AB,垂足为D.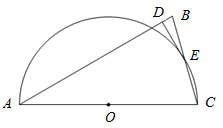 (1)、求证:点E是BC的中点;(2)、判断DE与⊙O的位置关系,并证明你的结论;(3)、如果⊙O的直径为9,cosB= , 求DE的长.
(1)、求证:点E是BC的中点;(2)、判断DE与⊙O的位置关系,并证明你的结论;(3)、如果⊙O的直径为9,cosB= , 求DE的长.
20. 贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).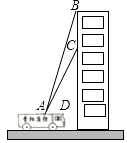 21. 湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 天的总成本为 万元;放养 天的总成本为 万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是 万元,收购成本为 万元,求 和 的值;(2)、
21. 湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 天的总成本为 万元;放养 天的总成本为 万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是 万元,收购成本为 万元,求 和 的值;(2)、设这批淡水鱼放养 天后的质量为 ( ),销售单价为 元/ .根据以往经验可知: 与 的函数关系为 ; 与 的函数关系如图所示.
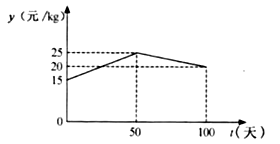
①分别求出当 和 时, 与 的函数关系式;
②设将这批淡水鱼放养 天后一次性出售所得利润为 元,求当 为何值时, 最大?并求出最大值.(利润=销售总额-总成本)
四、综合题
-
22. 如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0, ).
 (1)、求∠BAO的度数;(2)、如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?(3)、若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
(1)、求∠BAO的度数;(2)、如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?(3)、若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.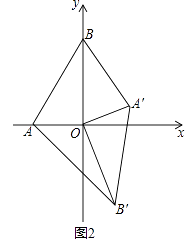 23. 在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.(1)、任意一对“互换点”能否都在一个反比例函数的图象上?为什么?(2)、M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);(3)、在抛物线y=x2+bx+c的图象上有一对“互换点”A、B,其中点A在反比例函数y=﹣ 的图象上,直线AB经过点P( , ),求此抛物线的表达式.
23. 在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.(1)、任意一对“互换点”能否都在一个反比例函数的图象上?为什么?(2)、M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);(3)、在抛物线y=x2+bx+c的图象上有一对“互换点”A、B,其中点A在反比例函数y=﹣ 的图象上,直线AB经过点P( , ),求此抛物线的表达式.