湖南省衡阳市2017届九年级上册数学期末考试试卷

试卷日期：2018-01-23 考试类型：期末考试

前去【出卷网】下载

一、单选题

1. 使二次根式 $\sqrt{2 - a}$ 有意义的a的取值范围是（）

A、a≥﹣2 B、a≥2 C、a≤2 D、a≤﹣2

查看试题解析
2. 若线段c满足 $\frac{a}{c} = \frac{c}{b}$ ，且线段a=4cm，b=9 cm，则线段c=（）

A、6cm B、7cm C、8cm D、9cm

查看试题解析
3. 下列方程中，不是一元二次方程的是（）

A、（x﹣1）x=1 B、 $\frac{1}{x^{2}} + \frac{1}{x} = 4$ C、3x²﹣5=0 D、2y（y﹣1）=4

查看试题解析
4. 关于x的一元二次方程 $2 x^{2} - 3 x - a^{2} + 1 = 0$ 的一个根为2，则 $a$ 的值是（）

A、 $1$ B、 $\sqrt{3}$ C、 $- \sqrt{3}$ D、 $\pm \sqrt{3}$

查看试题解析
5. 同时抛掷两枚均匀的硬币，落地后两枚硬币都是正面朝上的概率是（）

A、 $1$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
6. 在Rt△ABC中， $∠ C = 90 °$ ， $tan A = \frac{2}{3}$ ， $A C = 6$ ，则 $B C =$ （）。

A、9 B、4 C、18 D、12

查看试题解析
7. 下列命题中，正确的是（）

A、所有的等腰三角形都相似 B、所有的直角三角形都相似 C、所有的等边三角形都相似 D、所有的矩形都相似

查看试题解析
8. 抛物线y=﹣（x﹣2）²+3的对称轴是（）

A、直线x=﹣2 B、直线x=2 C、直线x=3 D、直线x=﹣3

查看试题解析
9. 在一个抽屉里放有a个除颜色不同其它完全相同的球，设a个球中红球只有3个，每次将球搅拌均匀后任意摸出一个，大量重复摸球实验后发现，摸到红球的频率稳定在25%左右．则抽屉里原有球（）个．

A、12 B、9 C、6 D、3

查看试题解析
10. 已知关于x的一元二次方程x²-m=2x有两个不相等的实数根，则m的取值范围是（）

A、m＞-1 B、m＜-2 C、m≥0 D、m＜0

查看试题解析
11. 如图，△ABC中，D为AB的中点，DE∥BC，则下列结论中错误的是（）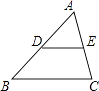

A、 $\frac{A D}{B D} = \frac{D E}{B C}$ B、 $\frac{A D}{B D} = \frac{A E}{E C}$ C、DE= $\frac{1}{2}$ BC D、S_△_ADE= $\frac{1}{3}$ S_四边形_BCED

查看试题解析
12. 如图，在矩形 $A B C D$ 中，P、R分别是BC和DC上的点，E，F分别是AP和RP的中点，当点P在BC上从点B向点C移动，而点R不动时，下列结论正确的是（）

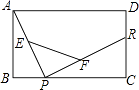A、线段EF的长逐渐增长 B、线段EF的长逐渐减小 C、线段EF的长始终不变 D、线段EF的长与点P的位置有关

查看试题解析

二、填空题

13. 化简： $\sqrt{18 a^{3}} =$ ；

查看试题解析
14. 方程 $2 x^{2} - 8 = 0$ 的解是；

查看试题解析
15. 在Rt△ABC中， $∠ C = 90 °$ ， $A C = B C$ ，那么 $sin A =$ ；

查看试题解析
16. 一元二次方程 $x^{2} + 5 x - 6 = 0$ 的两根和是；

查看试题解析
17. 如图，△ $A B C$ ∽△ $A_{1} B_{1} C_{1}$ ，那么它们的相似比是；

查看试题解析

三、解答题

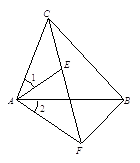
18. 计算：（ $\frac{1}{3}$ ）^﹣¹+16÷（﹣2）³+（2016﹣ $\frac{\sqrt{3}}{2}$ ）⁰﹣ $\sqrt{3}$ tan60°．

查看试题解析
19. 解方程：x²﹣10x+25=7．

查看试题解析
20. 先化简，再求值： $(\sqrt{2 x} + \sqrt{y}) (\sqrt{2 x} - \sqrt{y}) - {(\sqrt{2 x} - \sqrt{y})}^{2}$ ，其中 $x = 3$ ， $y = 4$

查看试题解析
21. 如图， $∠ 1= ∠ 2$ ， $A C = 6$ ， $A B = 12$ ， $A E = 4$ ， $A F = 8$ .试说明： $∠ A C E = ∠ A B F$

查看试题解析
22. 完全相同的四张卡片，上面分别标有数字1，2，﹣1，﹣2，将其背面朝上，从中任意抽出两张（不放回），把第一张的数字记为a，第二张的数字记为b，以a、b分别作为一个点的横坐标与纵坐标；求点（a，b）在第四象限的概率．（用树状图或列表法求解）

查看试题解析
23. 如图，AE是位于公路边的电线杆，为了使拉线CDE不影响汽车的正常行驶，电力部门在公路的另一边竖立了一根水泥撑杆BD，用于撑起拉线．已知公路的宽AB为8米，电线杆AE的高为12米，水泥撑杆BD高为6米，拉线CD与水平线AC的夹角为67.4°．求拉线CDE的总长L（A、B、C三点在同一直线上，电线杆、水泥杆的大小忽略不计）．（参考数据：sin67.4°≈ $\frac{12}{13}$ ，cos67.4°≈ $\frac{5}{13}$ ，tan67.4°≈ $\frac{12}{5}$ ）

查看试题解析
24. 某商店如果将进货价为8元的商品按每件10元售出，每天可销售200件，现在采用提高售价，减少进货量的方法增加利润，已知这种商品每涨价0.5元，其销量就减少10件．

(1)、要使每天获得利润700元，请你帮忙确定售价；

(2)、问售价定在多少时能使每天获得的利润最多？并求出最大利润．

查看试题解析
25. 如图，菱形ABCD的边长为24厘米，∠A=60°，点P从点A出发沿线路AB→BD作匀速运动，点Q从点D同时出发沿线路DC→CB→BA作匀速运动．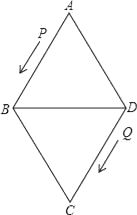

(1)、求BD的长；

(2)、已知点P、Q运动的速度分别为4厘米/秒，5厘米/秒，经过12秒后，P、Q分别到达M、N两点，若按角的大小进行分类，请你确定△AMN是哪一类三角形，并说明理由；

(3)、设（2）中的点P、Q分别从M、N同时沿原路返回，点P的速度不变，点Q的速度改变为a厘米/秒，经过3秒后，P、Q分别到达E、F两点，若△BEF与（2）中的△AMN相似，试求a的值．

查看试题解析
26. 如图，抛物线y=x²+bx+c的顶点为D（﹣1，﹣4），与y轴相交于点C（0，﹣3）与x轴交于A、B两点（点A在点B的左边），连接AC、CD、AD．

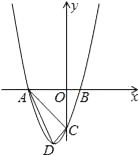(1)、求抛物线的解析式；

(2)、试证明△ACD为直角三角形；

(3)、若点E在抛物线的对称轴上，抛物线上是否存在点F，使得以A、B、E、F四点为顶点的四边形为平行四边形？若存在，求出满足条件的点F的坐标；若不存在，请说明理由．

查看试题解析