北京市通州区2016届九年级上学期数学期末考试试卷
试卷日期：2018-01-11 考试类型：期末考试
一、单选题
-
1. 已知点（-2，2）在二次函数y＝ax2的图象上，那么a的值是（ ）
A、1 B、2 C、 D、－2. 在Rt△ABC中，∠C=90°，AB=2BC，那么sinA的值为（ ）
A、 B、 C、 D、13. 如图是某几何体的三视图，那么这个几何体是（ ）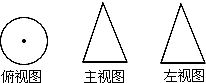
A、三菱锥 B、圆柱 C、球 D、圆锥4. 如图，⊙O的半径为5，AB为弦，OC⊥AB，垂足为C，如果OC=3，那么弦AB的长为（ ）
A、4 B、6 C、8 D、105. 如图，是一个正方体的表面展开图，那么原正方体中与“祝”字所在的面相对的面上标的字是（ ）
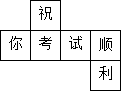A、考 B、试 C、顺 D、利6. 如果点M（-2，y1），N（-1，y2）在抛物线y=－x2+2x上，那么下列结论正确的是（ ）
A、y1＜y2 B、y1＞y2 C、y1≤y2 D、y1≥y2 ．7. 如图：为了测量某棵树的高度，小刚用长为2m的竹竿做测量工具，移动竹竿，使竹竿、树的顶端的影子恰好落在地面的同一点，此时，竹竿与这一点距离6m，与树相距15m，那么这棵的高度为（ ）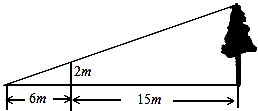
A、5米 B、7米 C、7.5米 D、21米8. 如果弧长为6π的弧所对的圆心角为60°，那么这条弧所在的圆的半径是（ ）A、18 B、12 C、36 D、69. 如图，AB是⊙O的切线，B为切点，AO的延长线交⊙O于点C，连接BC，如果∠A=30°，AB=2 ，那么AC的长等于（ ）
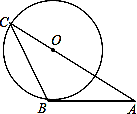A、4 B、6 C、4 D、610. 如图1，AD，BC是⊙O的两条互相垂直的直径，点P从点O出发沿图中某一个扇形顺时针匀速运动，设∠APB=y（单位：度），如果y与点P运动的时间x（单位：秒）的函数关系的图象大致如图2所示，那么点P的运动路线可能为（ ）
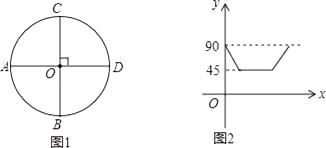A、O→B→A→O B、O→A→C→O C、O→C→D→O D、O→B→D→O二、填空题
-
11. 请写出一个开口向上，并且与y轴交于点（0，－1）的抛物线的表达式：
12. 把二次函数的表达式y=x2－4x+6化为y=a（x－h）2+k的形式，那么h+k= ．
13. 如图，边长为a的正方形发生形变后，成为边长为a的菱形，如果设这个菱形的一组对边之间的距离为h，记 =k，我们把k叫做这个菱形的“形变度”。如变形后的菱形有一个角是60°，那么形变度k= ．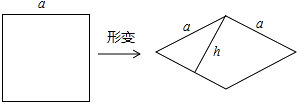
14. 学习相似三角形和解直角三角形的相关内容后，张老师请同学们交流这样的一个问题：“如上图，在正方形网格上有△A1B1C1和△A2B2C2 ， 这两个三角形是否相似？”，那么你认为△A1B1C1和△A2B2C2 ， （相似或不相似）；理由是 ．
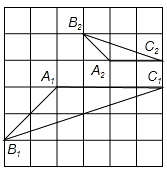15. 如图，弦AB的长等于⊙O的半径，那么弦AB所对的圆周角的度数是 ．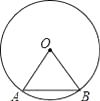
三、解答题
-
16. 小明四等分弧AB，他的作法如下：
①连接AB（如图）；作AB的垂直平分线CD交弧AB于点M，交AB于点T；
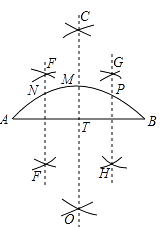
②分别作AT，TB的垂直平分线EF，GH，交弧AB于N，P两点，则N，M，P三点把弧AB四等分。你认为小明的作法是否正确： ， 理由是 。
17. 如图，已知∠1=∠2，∠AED=∠C，求证：△ABC∽△ADE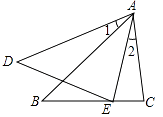
18. 已知二次函数y=x2+bx+c的图象过（2，-1）和（4，3）两点，求y=x2+bx+c的表达式
19. 已知：如图，A、B、C为⊙O上的三个点，⊙O的直径为4cm，∠ACB=45°，求AB的长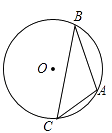
20. 如果三角形有一边上的中线恰好等于这边的长，那么称这个三角形为“有趣三角形”，这条中线称为“有趣中线”。如图，在三角形ABC中，∠C=90°，较短的一条直角边BC=1，且三角形ABC是“有趣三角形”，求三角形ABC的“有趣中线”的长。
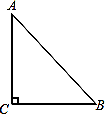21. 如图所示，以平行四边形ABCD的顶点A为圆心，AB为半径作圆，分别交BC，AD于E，F两点，交BA的延长于G，判断弧EF和弧FG是否相等，并说明理由。
22. 如图，在平行四边形ABCD中，E为CD上一点，连结AE，BD，且AE，BD交于点F，S△DEF∶S△ABF=4∶25，求DE∶EC的值．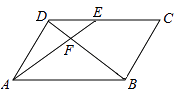
23. 如图是春运期间的一个回家场景。一种拉杆式旅行箱的示意图如图所示，箱体长AB=50cm，拉杆最大伸长距离BC=30cm，点A到地面的距离AD=8cm，旅行箱与水平面AE成60°角，求拉杆把手处C到地面的距离（精确到1cm）．（参考数据： ）
24. 综合题
(1)、抛物线m1：y1=a1x2+b1x+c1中，函数y1与自变量x之间的部分对应值如表：
设抛物线m1的顶点为P，与y轴的交点为C，则点P的坐标为 ， 点C的坐标为 ．
(2)、将设抛物线m1沿x轴翻折，得到抛物线m2：y2=a2x2+b2x+c2 ， 则当x=-3时，y2= ．
(3)、在（1）的条件下，将抛物线m1沿水平方向平移，得到抛物线m3 ． 设抛物线m1与x轴交于A，B两点（点A在点B的左侧），抛物线m3与x轴交于M，N两点（点M在点N的左侧）．过点C作平行于x轴的直线，交抛物线m3于点K．问：是否存在以A，C，K，M为顶点的四边形是菱形的情形？若存在，请求出点K的坐标；若不存在，请说明理由．
25. 如图，在平面直角坐标系xOy中，⊙A与y轴相切于点B（0， ），与x轴相交于M，N两点，如果点M的坐标为（ ，0），求点N的坐标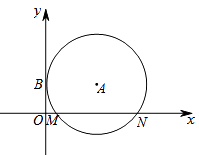
26. 根据下列要求，解答相关问题．
(1)、请补全以下求不等式﹣2x2﹣4x＞0的解集的过程．①构造函数，画出图象：根据不等式特征构造二次函数y=﹣2x2﹣4x；并在下面的坐标系中（图1）画出二次函数y=﹣2x2﹣4x的图象（只画出图象即可）．
②求得界点，标示所需，当y=0时，求得方程﹣2x2﹣4x=0的解为（ ）；并用锯齿线标示出函数y=﹣2x2﹣4x图象中y＞0的部分．
③借助图象，写出解集：由所标示图象，可得不等式﹣2x2﹣4x＞0的解集为﹣2＜x＜0．请你利用上面求一元一次不等式解集的过程，求不等式x2﹣2x+1≥4的解集．
27. 已知，如图，在R t△ABC中，∠C＝90°，∠BAC的角平分线AD交BC边于D．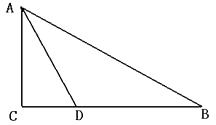
(1)、动手操作：利用尺规作，以AB边上一点O为圆心，过A，D两点作⊙O，与AB的另一个交点为E，与AC的另一个交点为F（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由。
(2)、若∠BAC=60度，CD= ，求线段BD、BE与劣弧DE所围成的图形面积．（结果保留根号和 ）
28. 王华在学习相似三角形时，在北京市义务教育课程改革实验教材第17册书，第31页遇到这样一道题：如图1，在△ABC中，P是边AB上的一点，联结CP．
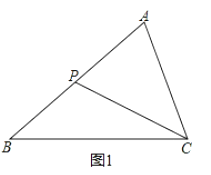
要使△ACP∽△ABC，还需要补充的一个条件是__，或__．
(1)、王华补充的条件是 ， 或 ．
(2)、请你参考上面的图形和结论，探究、解答下面的问题：如图2，在△ABC中，∠A=30°，AC2= AB2+AB．BC．
求∠C的度数．
29. 定义：P、Q分别是两条线段a和b上任意一点，线段PQ的长度的最小值叫做线段a与线段b的距离．已知O（0，0），A（4，0），B（m，n），C（m+4，n）是平面直角坐标系中四点．
(1)、根据上述定义，当m=2，n=2时，如图1，线段BC与线段OA的距离是；当m=5，n=2时，如图2，线段BC与线段OA的距离为；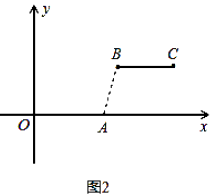
(2)、如图3，若点B落在圆心为A，半径为2的圆上，线段BC与线段OA的距离记为d，求d关于m的函数解析式．
(3)、当m的值变化时，动线段BC与线段OA的距离始终为2，线段BC的中点为M，①求出点M随线段BC运动所围成的封闭图形的周长；
②点D的坐标为（0，2），m≥0，n≥0，作MH⊥x轴，垂足为H，是否存在m的值使以A、M、H为顶点的三角形与△AOD相似？若存在，求出m的值；若不存在，请说明理由．