北京市顺义区2016届九年级上学期数学期末考试试卷
试卷日期:2018-01-11 考试类型:期末考试
一、单选题
-
1. ﹣ 的倒数是( )A、3 B、 C、﹣ D、﹣32. 计算 的结果是( )
A、 B、 C、 D、33. 不等式3x+2>﹣1的解集是( )
A、x>﹣ B、x<﹣ C、x>﹣1 D、x<﹣14. 下列银行标志中,既不是中心对称图形也不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
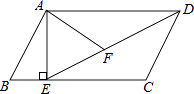
D、 5. 若3x=4y(xy≠0),则下列比例式成立的是( )A、= B、 C、 D、6. 在Rt△ABC中,∠C=90°,BC=3,AB=5,则cosA的值为( )A、 B、 C、 D、7. 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则 的值是( )
5. 若3x=4y(xy≠0),则下列比例式成立的是( )A、= B、 C、 D、6. 在Rt△ABC中,∠C=90°,BC=3,AB=5,则cosA的值为( )A、 B、 C、 D、7. 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则 的值是( ) A、 B、 C、 D、8. 如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是( )
A、 B、 C、 D、8. 如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是( )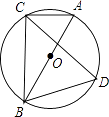 A、30° B、45° C、60° D、75°9. 若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A、30° B、45° C、60° D、75°9. 若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A、6, B、 ,3 C、6,3 D、 ,10. 如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
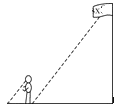
11. 分解因式:mn2+6mn+9m= .12. 一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9,这5个数据的中位数是 .13. 如图,身高是1.6m的某同学直立于旗杆影子的顶端处,测得同一时刻该项同学和旗杆的影子长分别为1.2m和9m,则旗杆的高度为 m.
14. 若反比例函数 的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是 .
15. 将抛物线y=2x2向下平移3个单位,再向左平移1个单位,所得抛物线的解析式为 .
16. 如图,在平面直角坐标系xOy中,△ABC外接圆的圆心坐标是 , 半径是 .
三、解答题
-
17. 计算:cos60°+tan30°•sin60°﹣(cos45°﹣ )° .18. 已知 ,求代数式 的值.19. 求二次函数y=x2﹣4x+3的顶点坐标及对称轴,并在所给坐标系中画出该二次函数的图象.
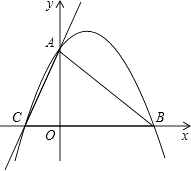
 20. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y= 的图象上,过点A的直线y=x+b交x轴于点B.
20. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y= 的图象上,过点A的直线y=x+b交x轴于点B.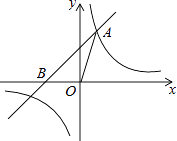 (1)、求k和b的值;
(1)、求k和b的值;
(2)、求△OAB的面积.
21. 李大叔想用篱笆围成一个周长为80米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)、求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)、当x是多少时,矩形场地面积S最大?最大面积是多少?22. 已知:如图,AB是⊙O的直径,弦 ,∠B=60°,OD⊥AC,垂足为D.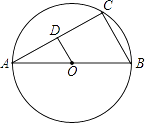 (1)、求OD的长;(2)、求劣弧AC的长.
(1)、求OD的长;(2)、求劣弧AC的长.
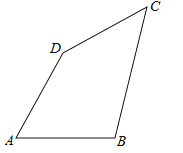
23.在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形周长为32,求BC和CD的长度.
 24. 一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈ )
24. 一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈ )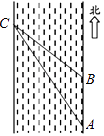 25. 已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴相交于A、B两点,且AB=2,求m的值.
25. 已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴相交于A、B两点,且AB=2,求m的值.
26. 在△ABC中,AB=6cm,AC=12cm,动点D以1cm/s 的速度从点A出发到点B止,动点E以2cm/s 的速度从点C出发到点A止,且两点同时运动,当以点A、D、E为顶点的三角形与△ABC相似时,求运动的时间t.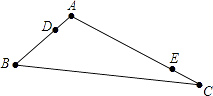 27. 如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
27. 如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.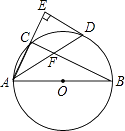 (1)、猜想ED与⊙O的位置关系,并证明你的猜想;(2)、若AB=6,AD=5,求AF的长.
(1)、猜想ED与⊙O的位置关系,并证明你的猜想;(2)、若AB=6,AD=5,求AF的长.