北京市石景山区2016届九年级上学期数学期末考试试卷
试卷日期:2018-01-11 考试类型:期末考试
一、选择题
-
1. 已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、不能确定2. 两个相似三角形的相似比为1:2,若较小三角形的面积为1,则较大三角形的面积为( )A、8 B、4 C、2 D、3. 德育处王主任将10份奖品分别放在10个完全相同的不透明礼盒中,准备将它们奖给小明等10位获“科技节活动先进个人”称号的同学.这些奖品中有5份是学习文具,3份是科普读物,2份是科技馆通票.小明同学从中随机取一份奖品,恰好取到科普读物的概率是( )
A、 B、 C、 D、4. 某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )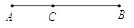 A、6.7m B、7.6m C、10m D、12.4m5. 将抛物线y=﹣(x+1)2向左平移1个单位后,得到的抛物线的顶点坐标是( )A、(﹣2,0) B、(0,0) C、(﹣1,﹣1) D、(﹣2,﹣1)6. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式中正确的是( )
A、6.7m B、7.6m C、10m D、12.4m5. 将抛物线y=﹣(x+1)2向左平移1个单位后,得到的抛物线的顶点坐标是( )A、(﹣2,0) B、(0,0) C、(﹣1,﹣1) D、(﹣2,﹣1)6. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式中正确的是( )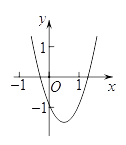 A、ac>0 B、b+2a<0 C、b2﹣4ac>0 D、a﹣b+c<07. 如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠AOC=80°,则∠D的度数为( )
A、ac>0 B、b+2a<0 C、b2﹣4ac>0 D、a﹣b+c<07. 如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠AOC=80°,则∠D的度数为( )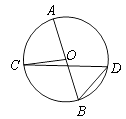 A、80° B、60° C、50° D、40°8. 如图,菱形ABCD中,对角线AC、BD交于点O,若AC=4,BD=2,则∠1的余弦值为( )
A、80° B、60° C、50° D、40°8. 如图,菱形ABCD中,对角线AC、BD交于点O,若AC=4,BD=2,则∠1的余弦值为( )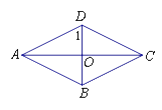 A、 B、 C、 D、9. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
A、 B、 C、 D、9. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( ) A、x=1 B、x=﹣1 C、x1=1,x2=﹣3 D、x1=1,x2=﹣410. 如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A、x=1 B、x=﹣1 C、x1=1,x2=﹣3 D、x1=1,x2=﹣410. 如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )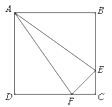 A、
A、 B、
B、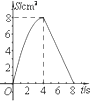 C、
C、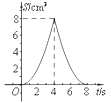 D、
D、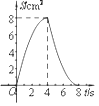
二、填空题
-
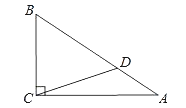
11. 如图,Rt△ABC中,∠ACB=90°,cosA= ,D为AB上一点,且AD:BD=1:2,若BC=3 ,求CD的长.
 12. 若 ,则锐角α= .
12. 若 ,则锐角α= .
13. 如图,在平面直角坐标系xOy中,点B在y轴上,AB=AO,反比例函数 的图象经过点A,若△ABO的面积为2,则k的值为 .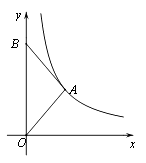 14. 如果某人沿坡度i=1:3的斜坡前进10m,那么他所在的位置比原来的位置升高了m.
14. 如果某人沿坡度i=1:3的斜坡前进10m,那么他所在的位置比原来的位置升高了m.
15. 如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,则扇面的面积为 (用代数式表示). 16. 根据函数学习中积累的知识与经验,请你构造一个函数,使其图象与x轴有交点,但与y轴无交点,这个函数表达式可以为 .
16. 根据函数学习中积累的知识与经验,请你构造一个函数,使其图象与x轴有交点,但与y轴无交点,这个函数表达式可以为 .
17. 如图,在平面直角坐标系xOy中,点A在y轴上,点B在x轴上,∠ABO=60°,若点D(1,0)且BD=2OD.把△ABO绕着点D逆时针旋转m°(0<m<180)后,点B恰好落在初始Rt△ABO的边上,此时的点B记为B′,则点B′的坐标为 .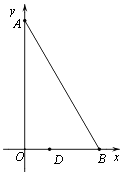
三、计算题
-
18. 计算:(3﹣π)0+4sin45°•cos30°﹣2﹣2 .
四、解答题
-
19. 已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)、求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;(2)、画出此函数图象的示意图.20. 《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果AB为⊙O的直径,弦CD⊥AB于E,AE=1寸,CD=10寸,那么直径AB的长为多少寸?”请你补全示意图,并求出AB的长. 21. 中秋节来临,小红家自己制作月饼.小红做了三个月饼,1个芝麻馅,2个豆沙馅;小红的爸爸做了两个月饼,1个芝麻馅,1个豆沙馅(除馅料不同,其它都相同).做好后他们请奶奶品尝月饼,奶奶从小红做的月饼中拿了一个,从小红爸爸做的月饼中拿了一个.请利用列表或画树状图的方法求奶奶拿到的月饼都是豆沙馅的概率.
21. 中秋节来临,小红家自己制作月饼.小红做了三个月饼,1个芝麻馅,2个豆沙馅;小红的爸爸做了两个月饼,1个芝麻馅,1个豆沙馅(除馅料不同,其它都相同).做好后他们请奶奶品尝月饼,奶奶从小红做的月饼中拿了一个,从小红爸爸做的月饼中拿了一个.请利用列表或画树状图的方法求奶奶拿到的月饼都是豆沙馅的概率.
22. 在平面直角坐标系xOy中,反比例函数 的图象过点A(1,6).(1)、求反比例函数的表达式;
(2)、过点A的直线与反比例函数 图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
23. 如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:①平面镜;②皮尺;③长为2米的标杆;④高为1.5m的测角仪(测量仰角、俯角的仪器),请根据你所设计的测量方案,回答下列问题:
 (1)、画出你的测量方案示意图,并根据你的测量方案写出你所选用的测量工具;
(1)、画出你的测量方案示意图,并根据你的测量方案写出你所选用的测量工具;
(2)、结合你的示意图,写出求电线杆高度的思路.24. “母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进了一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.在义卖的过程中发现“这种文化衫每天的销售件数y(件)与销售单价x(元)满足一次函数关系:y=﹣3x+108(20<x<36)”.如果义卖这种文化衫每天的利润为p(元),那么销售单价定为多少元时,每天获得的利润最大?最大利润是多少?
25. 如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC. (1)、求证:直线BC是⊙O的切线;(2)、若AE=2,tan∠DEO= ,求AO的长.
(1)、求证:直线BC是⊙O的切线;(2)、若AE=2,tan∠DEO= ,求AO的长.
26. 阅读下面材料:小天在学习锐角三角函数中遇到这样一个问题:在Rt△ABC中,∠C=90°,∠B=22.5°,则tan22.5°=
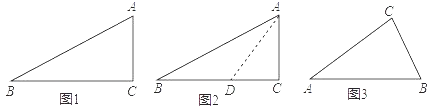
小天根据学习几何的经验,先画出了几何图形(如图1),他发现22.5°不是特殊角,但它是特殊角45°的一半,若构造有特殊角的直角三角形,则可能解决这个问题.于是小天尝试着在CB边上截取CD=CA,连接AD(如图2),通过构造有特殊角(45°)的直角三角形,经过推理和计算使问题得到解决.
请回答:
(1)、tan22.5°= .(2)、参考小天思考问题的方法,解决问题:如图3,在等腰△ABC 中,AB=AC,∠A=30°,请借助△ABC,构造出15°的角,并求出该角的正切值.
27. 在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.
(1)、求抛物线的表达式;(2)、点D(n,y1),E(3,y2)在抛物线上,若y1<y2 , 请直接写出n的取值范围;(3)、设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.
28. 在正方形ABCD中,DE为正方形的外角∠ADF的角平分线,点G在线段AD上,过点G作PG⊥DE于点P,连接CP,过点D作DQ⊥PC于点Q,交射线PG于点H.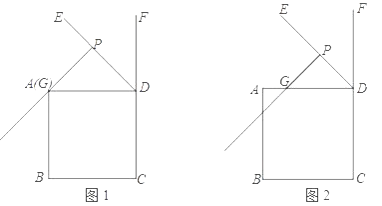 (1)、如图1,若点G与点A重合.
(1)、如图1,若点G与点A重合.①依题意补全图1;
②判断DH与PC的数量关系并加以证明;
(2)、如图2,若点H恰好在线段AB上,正方形ABCD的边长为1,请写出求DP长的思路(可以不写出计算结果).29. 在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度.图1为点P在⊙O外的情形示意图.
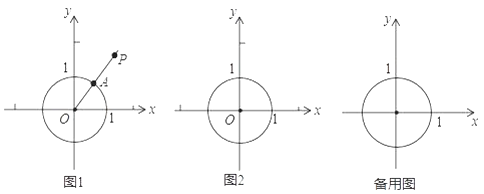 (1)、若点B(1,0),C(1,1),D(0, ),则SB=;SC=;SD=;
(1)、若点B(1,0),C(1,1),D(0, ),则SB=;SC=;SD=;
(2)、若直线y=x+b上存在点M,使得SM=2,求b的取值范围;(3)、已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR , 直接写出满足条件的线段PQ长度的最大值.
-