北京市门头沟区2016届九年级上学期数学期末考试试卷
试卷日期:2018-01-11 考试类型:期末考试
一、单选题
-
1. 如果4a=5b(ab≠0),那么下列比例式变形正确的是( )A、= B、= C、= D、=2. 在Rt△ABC中,如果∠C=90°,AB=10,BC=8,那么cosB的值是( )A、 B、 C、 D、3. 已知⊙O的半径为5,点P到圆心O的距离为8,那么点P与⊙O的位置关系是( )A、点P在⊙O上 B、点P在⊙O内 C、点P在⊙O 外 D、无法确定4. 小明的妈妈让他在无法看到袋子里糖果的情形下从袋子里抽出一颗糖果.袋子里有三种颜色的糖果,它们的大小、形状、质量等都相同,其中所有糖果的数量统计如图所示.小明抽到红色糖果的概率为( )
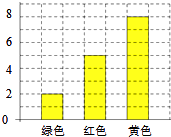 A、 B、 C、 D、5. 如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC= ,AC=3,则CD的长为( )
A、 B、 C、 D、5. 如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC= ,AC=3,则CD的长为( )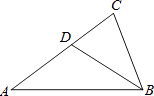 A、1 B、 C、2 D、6. 将抛物线y=5x2先向左平移2个单位,再向上平移3个单位后得到新的抛物线,则新抛物线的表达式是( )A、y=5(x+2)2+3 B、y=5(x﹣2)2+3 C、y=5(x﹣2)2﹣3 D、y=5(x+2)2﹣37. 已知点A(1,m)与点B(3,n)都在反比例函数y=图象上,那么m与n之间的关系是( )
A、1 B、 C、2 D、6. 将抛物线y=5x2先向左平移2个单位,再向上平移3个单位后得到新的抛物线,则新抛物线的表达式是( )A、y=5(x+2)2+3 B、y=5(x﹣2)2+3 C、y=5(x﹣2)2﹣3 D、y=5(x+2)2﹣37. 已知点A(1,m)与点B(3,n)都在反比例函数y=图象上,那么m与n之间的关系是( )
A、m>n B、m<n C、m≥n D、m≤n8. 如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )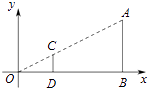 A、(3,1) B、(2,0) C、(3,3) D、(2,1)9. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
A、(3,1) B、(2,0) C、(3,3) D、(2,1)9. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )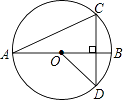 A、160° B、150° C、140° D、120°10. 如图,点C是以点O为圆心、AB为直径的半圆上的一个动点(点C不与点A、B重合),如果AB=4,过点C作CD⊥AB于D,设弦AC的长为x,线段CD的长为y,那么在下列图象中,能表示y与x函数关系的图象大致是( )
A、160° B、150° C、140° D、120°10. 如图,点C是以点O为圆心、AB为直径的半圆上的一个动点(点C不与点A、B重合),如果AB=4,过点C作CD⊥AB于D,设弦AC的长为x,线段CD的长为y,那么在下列图象中,能表示y与x函数关系的图象大致是( ) A、
A、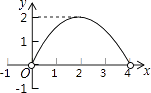 B、
B、 C、
C、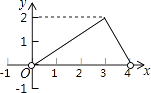 D、
D、
二、填空题
-
11. 如果两个相似三角形的相似比是1:3,那么这两个三角形面积的比是 .12. 颐和园是我国现存规模最大,保存最完整的古代皇家园林,它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园.该园有一个六角亭,如果它的地基是半径为2米的正六边形,那么这个地基的周长是米.
 13. 图1中的三翼式旋转门在圆形的空间内旋转,旋转门的三片旋转翼把空间等分成三个部分,图2是旋转门的俯视图,显示了某一时刻旋转翼的位置,根据图2中的数据,可知 的长是m.
13. 图1中的三翼式旋转门在圆形的空间内旋转,旋转门的三片旋转翼把空间等分成三个部分,图2是旋转门的俯视图,显示了某一时刻旋转翼的位置,根据图2中的数据,可知 的长是m.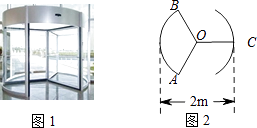 14. 写出一个图象位于二、四象限的反比例函数的表达式,y= .
14. 写出一个图象位于二、四象限的反比例函数的表达式,y= .
15. “圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 .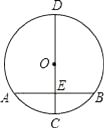
三、解答题
-
16. 学习了反比例函数的相关内容后,张老师请同学们讨论这样的一个问题:“已知反比例函数 ,当x>1时,求y的取值范围?”同学们经过片刻的思考和交流后,小明同学举手回答说:“由于反比例函数 的图象位于第四象限,因此y的取值范围是y<0.”你认为小明的回答是否正确: , 你的理由是: .17. 计算: |.18. 如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高.
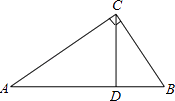 (1)、求证:△ABC∽△CBD;(2)、如果AC=4,BC=3,求BD的长.19. 已知二次函数y=x2﹣6x+5.(1)、将y=x2﹣6x+5化成y=a(x﹣h)2+k的形式;
(1)、求证:△ABC∽△CBD;(2)、如果AC=4,BC=3,求BD的长.19. 已知二次函数y=x2﹣6x+5.(1)、将y=x2﹣6x+5化成y=a(x﹣h)2+k的形式;
(2)、求该二次函数的图象的对称轴和顶点坐标;(3)、当x取何值时,y随x的增大而减小.20. 如图,在Rt△ABC中,∠ABC=90°,BC=1,AC= .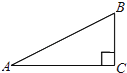 (1)、以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;(2)、求点A和点A′之间的距离.21. 如图,在平面直角坐标系xOy中,一次函数y=﹣2x的图象与反比例函数y= 的图象交于点A(﹣1,n).
(1)、以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;(2)、求点A和点A′之间的距离.21. 如图,在平面直角坐标系xOy中,一次函数y=﹣2x的图象与反比例函数y= 的图象交于点A(﹣1,n).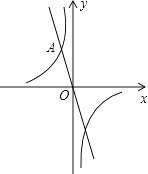 (1)、求反比例函数y= 的解析式;(2)、若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.22. “永定楼”是门头沟区的地标性建筑,某中学九年级数学兴趣小组进行了测量它高度的社会实践活动.如图,他们在A点测得顶端D的仰角∠DAC=30°,向前走了46米到达B点后,在B点测得顶端D的仰角∠DBC=45°.求永定楼的高度CD.(结果保留根号)
(1)、求反比例函数y= 的解析式;(2)、若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.22. “永定楼”是门头沟区的地标性建筑,某中学九年级数学兴趣小组进行了测量它高度的社会实践活动.如图,他们在A点测得顶端D的仰角∠DAC=30°,向前走了46米到达B点后,在B点测得顶端D的仰角∠DBC=45°.求永定楼的高度CD.(结果保留根号)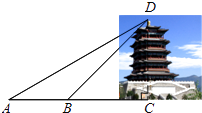 23. 已知二次函数y=mx2﹣(m+2)x+2(m≠0).(1)、求证:此二次函数的图象与x轴总有交点;(2)、如果此二次函数的图象与x轴两个交点的横坐标都是整数,求正整数m的值.24. 如图,在四边形ABCD中,AB∥CD,过点C作CE∥AD交AB于E,连接AC、DE,AC与DE交于点F.
23. 已知二次函数y=mx2﹣(m+2)x+2(m≠0).(1)、求证:此二次函数的图象与x轴总有交点;(2)、如果此二次函数的图象与x轴两个交点的横坐标都是整数,求正整数m的值.24. 如图,在四边形ABCD中,AB∥CD,过点C作CE∥AD交AB于E,连接AC、DE,AC与DE交于点F.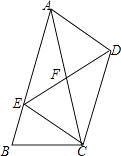 (1)、求证:四边形AECD为平行四边形;(2)、如果EF=2 ,∠FCD=30°,∠FDC=45°,求DC的长.25. 已知二次函数y1=x2+2x+m﹣5.(1)、如果该二次函数的图象与x轴有两个交点,求m的取值范围;
(1)、求证:四边形AECD为平行四边形;(2)、如果EF=2 ,∠FCD=30°,∠FDC=45°,求DC的长.25. 已知二次函数y1=x2+2x+m﹣5.(1)、如果该二次函数的图象与x轴有两个交点,求m的取值范围;
(2)、如果该二次函数的图象与x轴交于A、B两点,与y轴交于点C,且点B的坐标为(1,0),求它的表达式和点C的坐标;
(3)、如果一次函数y2=px+q的图象经过点A、C,请根据图象直接写出y2<y1时,x的取值范围.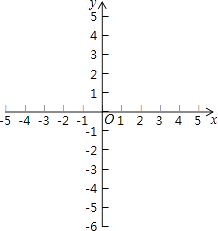 26. 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.
26. 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.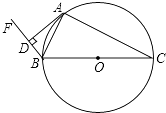 (1)、求证:AD为⊙O的切线;(2)、若BD=1,tan∠BAD= ,求⊙O的直径.27. 在平面直角坐标系xOy中,抛物线 经过点A(0,2)和B(1, ).(1)、求该抛物线的表达式;(2)、已知点C与点A关于此抛物线的对称轴对称,点D在抛物线上,且点D的横坐标为4,求点C与点D的坐标;(3)、在(2)的条件下,将抛物线在点A,D之间的部分(含点A,D)记为图象G,如果图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,求t的取值范围.
(1)、求证:AD为⊙O的切线;(2)、若BD=1,tan∠BAD= ,求⊙O的直径.27. 在平面直角坐标系xOy中,抛物线 经过点A(0,2)和B(1, ).(1)、求该抛物线的表达式;(2)、已知点C与点A关于此抛物线的对称轴对称,点D在抛物线上,且点D的横坐标为4,求点C与点D的坐标;(3)、在(2)的条件下,将抛物线在点A,D之间的部分(含点A,D)记为图象G,如果图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,求t的取值范围.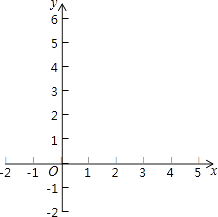 28. 在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
28. 在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:如果y′= ,那么称点Q为点P的“关联点”.
例如:点(5,6)的“关联点”为点(5,6),点(﹣5,6)的“关联点”
为点(﹣5,﹣6).
(1)、①点(2,1)的“关联点”为;②如果点A(3,﹣1),B(﹣1,3)的“关联点”中有一个在函数 的图象上,那么这个点是(填“点A”或“点B”).(2)、①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”,那么点M的坐标为;②如果点N*(m+1,2)是一次函数y=x+3图象上点N的“关联点”,求点N的坐标 .
(3)、如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,其“关联点”Q的纵坐标y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是 .
 29. 在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠PAB=α.(1)、依题意补全图1;(2)、如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;
29. 在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠PAB=α.(1)、依题意补全图1;(2)、如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;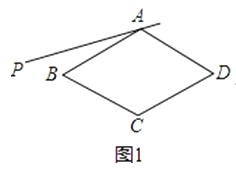 (3)、如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)
(3)、如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)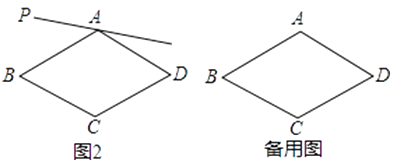 (4)、如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系.
(4)、如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系.