北京市丰台区2016届九年级上学期数学期末考试试卷
试卷日期:2018-01-11 考试类型:期末考试
一、单选题
-
1. 如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
 A、 B、 C、 D、2. 如图,在△ABC中,D,E分别是AB,AC上的点,且DE∥BC,若AD:DB=3:2,则AE:AC等于( )
A、 B、 C、 D、2. 如图,在△ABC中,D,E分别是AB,AC上的点,且DE∥BC,若AD:DB=3:2,则AE:AC等于( )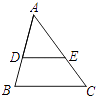 A、3:2 B、3:1 C、2:3 D、3:53. ⊙O的半径为3cm,如果圆心O到直线l的距离为d,且d=5cm,那么⊙O和直线l的位置关系是( )
A、3:2 B、3:1 C、2:3 D、3:53. ⊙O的半径为3cm,如果圆心O到直线l的距离为d,且d=5cm,那么⊙O和直线l的位置关系是( )
A、相交 B、相切 C、相离 D、不确定4. 抛物线y=(x﹣2)2+3的顶点坐标是( )A、(2,3) B、(﹣2,3) C、(2,﹣3) D、(﹣2,﹣3)5. 如果△ABC∽△DEF,相似比为2:1,且△DEF的面积为4,那么△ABC的面积为( )A、1 B、4 C、8 D、166.如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BAD的度数是( )
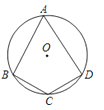 A、30° B、60° C、80° D、120°7. 对于反比例函数 , 下列说法正确的是( )A、图象经过点(2,﹣1) B、图象位于第二、四象限 C、当x<0时,y随x的增大而减小 D、当x>0时,y随x的增大而增大8. 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )
A、30° B、60° C、80° D、120°7. 对于反比例函数 , 下列说法正确的是( )A、图象经过点(2,﹣1) B、图象位于第二、四象限 C、当x<0时,y随x的增大而减小 D、当x>0时,y随x的增大而增大8. 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )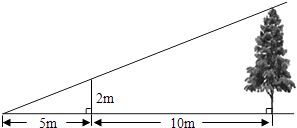 A、5m B、6m C、7m D、8m9. 小宏用直角三角板检查某些工件的弧形凹面是否是半圆,下列工件的弧形凹面一定是半圆的是( )A、
A、5m B、6m C、7m D、8m9. 小宏用直角三角板检查某些工件的弧形凹面是否是半圆,下列工件的弧形凹面一定是半圆的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,点A,B,C,D,E,F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )
10. 如图,点A,B,C,D,E,F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )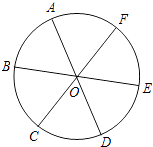 A、
A、 B、
B、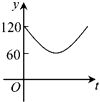 C、
C、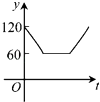 D、
D、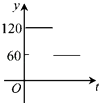
二、填空题
-
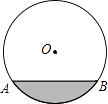
11. 如果∠A是锐角,且sinA= ,那么∠A=゜.12. 若2x=5y,则 = .13. 圆心角是60°的扇形的半径为6,则这个扇形的面积是 .14. 排水管的截面为如图所示的⊙O,半径为5m,如果圆心O到水面的距离是3m,那么水面宽AB=m.
 15. 请写出一个符合以下三个条件的二次函数的解析式: .
15. 请写出一个符合以下三个条件的二次函数的解析式: .①过点(1,1);
②当x>0时,y随x的增大而减小;
③当自变量的值为3时,函数值小于0.
三、解答题
-
16. 阅读下面材料:
在数学课上,老师请同学思考如下问题:
请利用直尺和圆规确定圆中弧AB所在圆的圆心

小亮的作法如下:
如图:
① 在弧AB上任意取一点C,分别连接AC,BC
②分别作AC,BC的垂直平分线,两条垂线平分线交于O点,所以点O就是所求弧AB的圆心
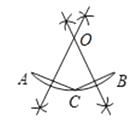
老师说:“小亮的作法正确.”
请你回答:小亮的作图依据是 .
17. 计算:2cos30°﹣tan45°+sin60°.18. 函数y=mx3m﹣1+4x﹣5是二次函数.(1)、求m的值;(2)、写出这个二次函数图象的对称轴:;将解析式化成y=a(x﹣h)2+k的形式为: .19. 如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.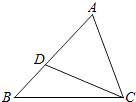 (1)、求证:△ACD∽△ABC;(2)、若AD=6,AB=10,求AC的长.20. 如图,直线y1=x+2与双曲线 相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.
(1)、求证:△ACD∽△ABC;(2)、若AD=6,AB=10,求AC的长.20. 如图,直线y1=x+2与双曲线 相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1. (1)、求k的值;(2)、若y1<y2 , 请你根据图象确定x的取值范围.21. 如图,某小区在规划改造期间,欲拆除小区广场边的一根电线杆AB,已知距电线杆AB水平距离14米处是观景台,即BD=14米,该观景台的坡面CD的坡角∠CDF的正切值为2,观景台的高CF为2米,在坡顶C处测得电线杆顶端A的仰角为30°,D、E之间是宽2米的人行道,如果以点B为圆心,以AB长为半径的圆形区域为危险区域.请你通过计算说明在拆除电线杆AB时,人行道是否在危险区域内?( ≈1.73)
(1)、求k的值;(2)、若y1<y2 , 请你根据图象确定x的取值范围.21. 如图,某小区在规划改造期间,欲拆除小区广场边的一根电线杆AB,已知距电线杆AB水平距离14米处是观景台,即BD=14米,该观景台的坡面CD的坡角∠CDF的正切值为2,观景台的高CF为2米,在坡顶C处测得电线杆顶端A的仰角为30°,D、E之间是宽2米的人行道,如果以点B为圆心,以AB长为半径的圆形区域为危险区域.请你通过计算说明在拆除电线杆AB时,人行道是否在危险区域内?( ≈1.73)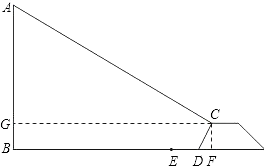 22. 如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
22. 如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.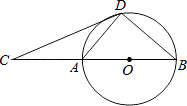 (1)、求证:CD是⊙O的切线;(2)、过点B作⊙O的切线交CD的延长线于点E,若AB=6,tan∠CDA= ,依题意补全图形并求DE的长.23. 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
(1)、求证:CD是⊙O的切线;(2)、过点B作⊙O的切线交CD的延长线于点E,若AB=6,tan∠CDA= ,依题意补全图形并求DE的长.23. 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:t(秒)
0
0.16
0.2
0.4
0.6
0.64
0.8
…
x(米)
0
0.4
0.5
1
1.5
1.6
2
…
y(米)
0.25
0.378
0.4
0.45
0.4
0.378
0.25
…
(1)、如果y是t的函数,①如图,在平面直角坐标系tOy中,描出了上表中y与t各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
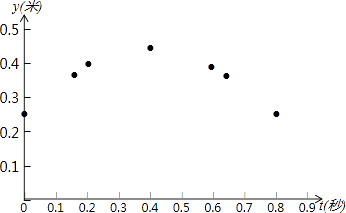
②当t为何值时,乒乓球达到最大高度?
(2)、如果y是关于x的二次函数,那么乒乓球第一次落在桌面时,与端点A的水平距离是多少? 24. 如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.
24. 如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.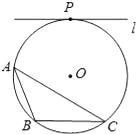 (1)、请仅用无刻度的直尺,在⊙O中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法);(2)、请写出证明△ABC被所作弦分成的两部分面积相等的思路.25. 已知抛物线G1:y=ax2+bx+c的顶点为(2,﹣3),且经过点(4,1).
(1)、请仅用无刻度的直尺,在⊙O中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法);(2)、请写出证明△ABC被所作弦分成的两部分面积相等的思路.25. 已知抛物线G1:y=ax2+bx+c的顶点为(2,﹣3),且经过点(4,1). (1)、求抛物线G1的解析式;
(1)、求抛物线G1的解析式;
(2)、将抛物线G1先向左平移3个单位,再向下平移1个单位后得到抛物线G2 , 且抛物线G2与x轴的负半轴相交于A点,求A点的坐标;
(3)、如果直线m的解析式为 ,点B是(2)中抛物线G2上的一个点,且在对称轴右侧部分(含顶点)上运动,直线n过点A和点B.问:是否存在点B,使直线m、n、x轴围成的三角形和直线m、n、y轴围成的三角形相似?若存在,求出点B的坐标;若不存在,请说明理由.
26. 在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)、 如图1,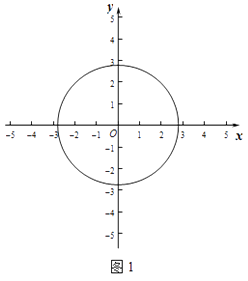
如果⊙O的半径为 ,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)、 如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.