北京市平谷区2015-2016学年八年级上学期数学期末考试试卷
试卷日期:2018-01-11 考试类型:期末考试
一、单选题
-
1. 京剧是我国的国粹,剪纸是流传已久的民间艺术,这两者的结合无疑是最能代表中国特色的艺术形式之一.图中京剧脸谱剪纸中是轴对称图形的个数是( )
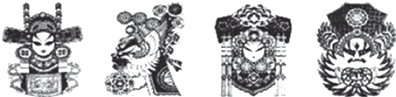 A、1个 B、2个 C、3个 D、4个2. 下列各式中,与分式 的值相等的是( )A、 B、 C、- D、3. 如果式子 有意义,那么x的取值范围在数轴上表示出来,正确的是( )A、
A、1个 B、2个 C、3个 D、4个2. 下列各式中,与分式 的值相等的是( )A、 B、 C、- D、3. 如果式子 有意义,那么x的取值范围在数轴上表示出来,正确的是( )A、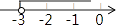 B、
B、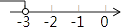 C、
C、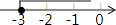 D、
D、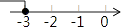 4. 如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
4. 如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )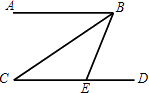 A、17° B、34° C、56° D、68°5. 在实数0,π, , ,- 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个6. 寒假即将来临,小明要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明选择到甲社区参加实践活动的可能性为( )A、 B、 C、 D、7. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、8. 为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )
A、17° B、34° C、56° D、68°5. 在实数0,π, , ,- 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个6. 寒假即将来临,小明要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明选择到甲社区参加实践活动的可能性为( )A、 B、 C、 D、7. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、8. 为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )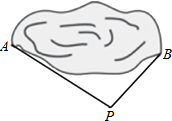 A、15m B、17m C、20m D、28m9. 已知 是正整数,则实数n的最大值为( )A、12 B、11 C、8 D、310. 小米在用尺规作图作△ABC边AC上的高BH,作法如下:
A、15m B、17m C、20m D、28m9. 已知 是正整数,则实数n的最大值为( )A、12 B、11 C、8 D、310. 小米在用尺规作图作△ABC边AC上的高BH,作法如下:①分别以点D,E为圆心,大于 DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
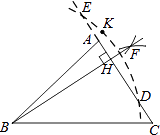
所以,BH就是所求作的高.
其中顺序正确的作图步骤是( )
A、①②③④ B、④③②① C、②④③① D、④③①②二、填空题
-
11. 计算: = .12. 若分式 值为0,则a的值为 .13. 若 a,b为两个连续的正整数,且 ,则a+b= .14. 如图,在△ABC中,∠C=90°,AC= ,点D在BC上,∠ADC=2∠B,AD=2,则BC= .
 15. 若实数x,y满足 =0,则代数式yx的值是 .16. 等腰三角形的两边长分别是3和5,则这个等腰三角形的周长为 .17. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是6,则AB= , AC= .
15. 若实数x,y满足 =0,则代数式yx的值是 .16. 等腰三角形的两边长分别是3和5,则这个等腰三角形的周长为 .17. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是6,则AB= , AC= .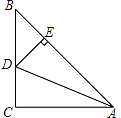 18. 阅读下面材料:
18. 阅读下面材料:在数学课上,老师提出如下问题:
尺规作图:作∠A′O′B′=∠AOB
已知:∠AOB
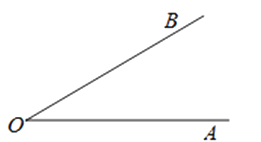
求作:∠A′O′B′=∠AOB
小米的作法如下:
① 作射线O′A′
② 以O为圆心,任意长为半径作弧,交OA于点C,交OB于点D
③ 以O′为圆心,OC为半径作弧C′E′,交O′A′于点C,
④ 以C′为圆心,CD为半径作弧,交C′E′于点D′
⑤ 过点D′做射线O′B′所以∠A′O′B′就是所求的角
如图:
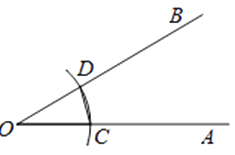

请回答:小米的作图依据是 .
三、解答题
-
19. 已知:如图,在△ABC中,AB=AC,点D,E在边BC上,且BD=CE.
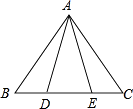
求证:AD=AE.
20. 计算: .21. 计算: .22. 计算: .23. 解方程:24. 已知 ,求代数式 的值.25. 有一块面积为150亩的绿化工程面向全社会公开招标.现有甲、乙两工程队前来竞标,甲队计划比规定时间少一半,乙队按规划时间完成.甲队比乙队每天多绿化10亩,问:规定时间是多少天?
26. 小明解方程 的过程如图.请指出他解答过程中的错误步骤及错误原因,并写出正确的解答过程.解:方程两边同乘x得1﹣(x﹣2)=1.…①
去括号得1﹣x﹣2=1.…②
合并同类项得﹣x﹣1=1.…③
移项得﹣x=2.…④
解得x=﹣2.…⑤
所以原方程的解为x=﹣2.…⑥
27. 如图,已知△ABC中AB=AC.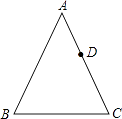 (1)、作图:在AC上有一点D,延长BD,并在BD的延长线上取点E,使AE=AB,连AE,作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(1)、作图:在AC上有一点D,延长BD,并在BD的延长线上取点E,使AE=AB,连AE,作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(2)、在(1)的条件下,连接CF,求证:∠E=∠ACF.
28. 阅读材料,解答下列问题.例:当a>0时,如a=6,则|a|=|6|=6,故此时|a|是它本身;当a=0时,|a|=0,故此时|a|是零;
当a<0时,如a=﹣6,则|a|=|﹣6|=6=﹣(﹣6),故此时|a|是它的相反数.
综上所述,|a|可分三种情况,即|a|=
这种分析方法渗透了数学的分类讨论思想.
问:
(1)、请仿照例中的分类讨论的方法,分析二次根式 的各种展开的情况.(2)、猜想 与|a|的大小关系是 |a|.
(3)、当1<x<2时,试化简: .29. 如图1,有两个全等的直角三角形△ABC和△EDF,∠ACB=∠F=90°,∠A=∠E=30°,点D在边AB上,且AD=BD=CD.△EDF绕着点D旋转,边DE,DF分别交边AC于点M,K.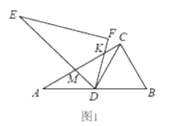 (1)、如图2、图3,当∠CDF=0°或60°时,AM+CKMK(填“>”,“<”或“=”),你的依据是;
(1)、如图2、图3,当∠CDF=0°或60°时,AM+CKMK(填“>”,“<”或“=”),你的依据是;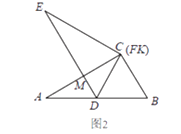
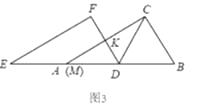 (2)、如图4,当∠CDF=30°时,AM+CKMK(填“>”或“<”);
(2)、如图4,当∠CDF=30°时,AM+CKMK(填“>”或“<”);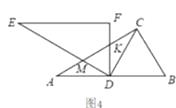 (3)、猜想:如图1,当0°<∠CDF<60°时,AM+CKMK,试证明你的猜想..
(3)、猜想:如图1,当0°<∠CDF<60°时,AM+CKMK,试证明你的猜想..