北京市怀柔区2015-2016学年八年级上学期数学期末考试试卷

试卷日期：2018-01-11 考试类型：期末考试

前去【出卷网】下载

一、单选题

1. 9的算术平方根是（）

A、3 B、﹣3 C、±3 D、± $\frac{1}{3}$

查看试题解析
2. 若 $\sqrt{x - 2}$ 表示二次根式，则x的取值范围是（）

A、x≤2 B、x≥2 C、x＜2 D、x＞2

查看试题解析
3. 若分式 $\frac{x - 1}{x + 2}$ 的值为0，则x的值是（）

A、﹣2 B、﹣1 C、0 D、1

查看试题解析
4. 剪纸是我国最古老的民间艺术之一，被列入第四批《人类非物质文化遗产代表作名录》，下列剪纸作品中，是轴对称图形的为（）

A、 B、 C、 D、

查看试题解析
5. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{4}$ C、 $\sqrt{3}$ D、 $\sqrt{8}$

查看试题解析
6. 下列各式计算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ B、4 $\sqrt{3}$ ﹣3 $\sqrt{3}$ =1 C、2 $\sqrt{3}$ ×3 $\sqrt{3}$ =6 $\sqrt{3}$ D、 $\sqrt{27}$ ÷ $\sqrt{3}$ =3

查看试题解析
7. 在一个不透明的箱子里，装有3个黄球、5个白球、2个黑球，它们除了颜色之外没有其他区别．从箱子里随意摸出1个球，则摸出白球的可能性大小为（　　）

A、0.2 B、0.5 C、0.6 D、0.8

查看试题解析
8. 如图，一块三角形玻璃损坏后，只剩下如图所示的残片，对图中的哪些数据测量后就可到建材部门割取符合规格的三角形玻璃（）

A、∠A，∠B，∠C B、∠A，线段AB，∠B C、∠A，∠C，线段AB D、∠B，∠C，线段AD

查看试题解析
9. 如图是由线段AB，CD，DF，BF，CA组成的平面图形，∠D=28°，则∠A+∠B+∠C+∠F的度数为（）

A、62° B、152° C、208° D、236°

查看试题解析
10. 如图，直线L上有三个正方形a，b，c，若a，c的面积分别为1和9，则b的面积为（）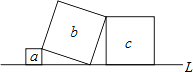

A、8 B、9 C、10 D、11

查看试题解析

二、填空题

11. 如果分式 $\frac{2}{x + 3}$ 有意义，那么x的取值范围是．

查看试题解析
12. 若实数x，y满足 $\sqrt{x - 2} + {(y - \sqrt{3})}^{2} = 0$ ，则代数式x+y的值是．

查看试题解析
13. 如果三角形的两条边长分别为23cm和10cm，第三边与其中一边的长相等，那么第三边的长为cm．

查看试题解析
14. 若a＜1，化简 $\sqrt{{(a - 1)}^{2}} - 1$ 等于．

查看试题解析
15. 已知 $\frac{1}{x} - \frac{1}{y} = 2$ ，则分式 $\frac{3 x + 2 x y - 3 y}{x - 2 x y - y}$ 的值等于．

查看试题解析
16. 在△ABC中，AB=4，AC=3，AD是△ABC的角平分线，则△ABD与△ACD的面积之比是．

查看试题解析

三、解答题

17. 阅读下面材料：
在数学课上，老师提出如下问题：∠AOB
尺规作图：做一个角等于已知角
已知：∠AOB
求做：一个角，使它等于∠AOB
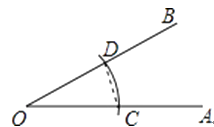
小强的作法如下：
① 作射线O′A'
② 以O为圆心，任意长为半径作弧，交OA于C，交OB于D
③ 以O′为圆心，OC为半径作弧C′E′，交弧O′A′于C′
④ 以C′为圆心，CD为半径作弧，交弧C′E′于D′
⑤过点D′作射线O′B′
所以∠A′O′B′就是所求的角
老师说：“小强的作法正确．”
请回答：小强用直尺和圆规作图∠A′O′B′=∠AOB，根据三角形全等的判定方法中的，
得出△D′O′C′≌△DOC，才能证明∠A′O′B′=∠AOB．

查看试题解析
18. 计算： $\sqrt{9} - \sqrt[3]{8} + | - \sqrt{2} | - {(\sqrt{3} - \sqrt{2})}^{0}$ ．

查看试题解析
19. 计算： $\sqrt{8} \times \sqrt{3} \div \sqrt{12} - \sqrt{\frac{1}{2}}$ ．

查看试题解析
20. 计算： $(\sqrt{2} + 1) \times (\sqrt{6} - \sqrt{3})$ ．

查看试题解析
21. 计算： $(a - 1 + \frac{1}{a + 1}) \cdot \frac{a + 1}{a}$ ．

查看试题解析
22. 如图，在Rt△ABC中，∠BAC=90°，点D在BC边上，且△ABD是等边三角形．若AB=2，求BC的长．

查看试题解析
23. 解分式方程： $\frac{1}{x - 1} + \frac{2 x}{x + 1} = 2$ ．

查看试题解析
24. 如图，点C，D在线段BF上，AB∥DE，AB=DF，∠A=∠F，求证：BC=DE．

查看试题解析
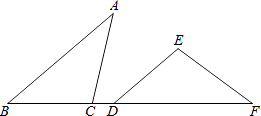25. 先化简： $(a - \frac{2 a - 1}{a}) \div \frac{1 - a^{2}}{a^{2} + a}$ ，然后从﹣1，0，1，2中选一个你认为合适的a值，代入求值．

查看试题解析
26. 小红家最近新盖了房子，室内装修时，木工师傅让小红爸爸去建材市场买一块长3m，宽2.2m的薄木板用来做家居面，到了市场爸爸看到满足这个尺寸的木板有点大，买还是不买爸爸犹豫了，因为他知道他家门框高只有2m，宽只有1m，他不知道这块木板买回家后能不能完整的通过自家门框．请你替小红爸爸解决一下难题，帮他算一算要买的木板能否通过自家门框进入室内．（备用图可供做题参考，薄木板厚度可以忽略不计）

查看试题解析
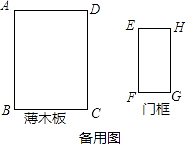27. 列方程解应用题
李明和王军相约周末去怀柔图书馆看书，请根据他们的微信聊天内容求李明乘公交、王军骑自行车每小时各行多少公里？

查看试题解析
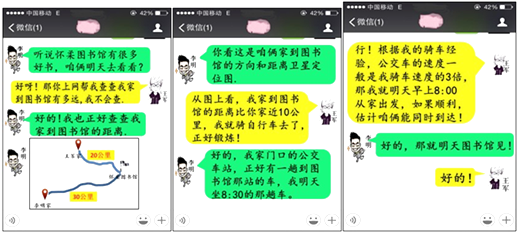28. 已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH与BE相交于点G．

(1)、判断AC与图中的那条线段相等，并证明你的结论；

(2)、若CE的长为 $\sqrt{3}$ ，求BG的长．

查看试题解析
29. 已知：在△ABC中，D为BC边上一点，B，C两点到直线AD的距离相等．

(1)、如图1，若△ABC是等腰三角形，AB=AC，则点D的位置在；

(2)、如图2，若△ABC是任意一个锐角三角形，猜想点D的位置是否发生变化，请补全图形并加以证明；

(3)、如图3，当△ABC是直角三角形，∠A=90°，并且点D满足（2）的位置条件，用等式表示线段AB，AC，AD之间的数量关系并加以证明．

查看试题解析
30. 请阅读下列材料：
问题：如图1，点A，B在直线l的同侧，在直线l上找一点P，使得AP+BP的值最小．
小明的思路是：如图2所示，先作点A关于直线l的对称点A′，使点A′，B分别位于直线l的两侧，再连接A′B，根据“两点之间线段最短”可知A′B与直线l的交点P即为所求．
请你参考小明同学的思路，探究并解决下列问题：

(1)、如图3，在图2的基础上，设AA'与直线l的交点为C，过点B作BD⊥l，垂足为D．若CP=1，AC=1，PD=2，直接写出AP+BP的值；

(2)、将（1）中的条件“AC=1”去掉，换成“BD=4﹣AC”，其它条件不变，直接写出此时AP+BP的值；

(3)、请结合图形，求 $\sqrt{{(m - 3)}^{2} + 1} + \sqrt{{(9 - m)}^{2} + 4}$ 的最小值．

查看试题解析