河南省南阳市淅川县2016届九年级上学期数学期末考试试卷
试卷日期：2017-12-29 考试类型：期末考试
一、单选题
-
1. 若式子 在实数范围内有意义，则x的取值范围是（ ）
A、x=1 B、x≥1 C、x＞1 D、x＜12. 已知△ABC∽△DEF，且AB：DE=1：2，则△ABC与△DEF的周长之比为（ ）A、1：2 B、2：1 C、1：4 D、4：33. 在直角三角形ABC中，已知∠C=90°，∠A=40°，BC=3，则AC=（ ）
A、3sin40° B、3sin50° C、3tan40° D、3tan50°4. 在一个不透明的口袋中装有若干个只有颜色不同的珠，如果口袋中只装有2个黄球且摸出黄球的概率为 ，那么袋中其他颜色的球共有（ ）A、1个 B、2个 C、3个 D、4个5. 在同一平面直角坐标系内，将函数y=2x2+4x﹣3的图象向右平移2个单位，再向下平移1个单位得到图象的顶点坐标是（ ）
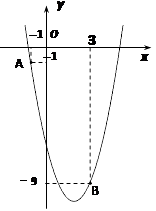
A、（﹣3，﹣6） B、（1，﹣4） C、（1，﹣6） D、（﹣3，﹣4）6. 小明从如图所示的二次函数y=ax2+bx+c的图象中，观察得出了下面五条信息：（1）a＜O；（2）b2﹣4ac＜0；（3）b＞O；（4）a+b+c＞0；（5）a﹣b+c＞0．你认为其中正确信息的个数有（ ）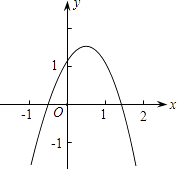
A、2个 B、3个 C、4个 D、5个7. 如图，△ABC的边AC与⊙O相交于C、D两点，且经过圆心O，边AB与⊙O相切，切点为B．已知∠A=30°，则∠C的大小是（ ）
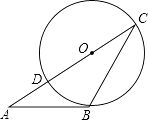A、30° B、45° C、60° D、40°二、填空题
-
8. 对于任意实数k，关于x的方程x2﹣2（k+1）x﹣k2+2k﹣1=0的根的情况为 ．
9. 如图，在△ABC中D、E两点分别在BC、AC边上，若BD=CD，∠B=∠CDE，DE=2，则AB的长度是 ．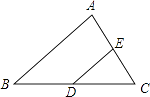
10. 如图是拦水坝的横断面．斜坡AB的坡度为1：2，BC⊥AE，垂足为点C，AC长为12米，则斜坡AB的长为米．
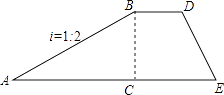11. 如图，在等边△ABC中，O为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3．CE=2，则AB的长为 ．
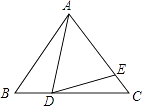12. 小明有黑色、白色、蓝色西服各一件，有红色、黄色领带各一条，从中分别取一件西服和一条领带，则小明穿黑色西服打红色领带的概率是 ．
13. 已知0≤x≤ ，那么函数y=﹣2x2+8x﹣6的最大值是 ．
14. 已知圆锥的母线长为6cm，底面圆的半径为3cm，则此圆锥侧面展开图的圆心角的度数是 ．
三、解答题
-
15. 计算题(1)、计算： （ ﹣ ）﹣ ﹣| ﹣3|(2)、计算：（﹣1）2014﹣ sin45°+（π﹣3.14）0(3)、解方程：2x2+x﹣6=0．16. 电动自动车已成为市民日常出行的首选工具．据某市某品牌电动自行车经销商1至3月份统计，该品牌电动自行车1月份销售150辆，3月份销售216辆．(1)、求该品牌电动自行车销售量的月均增长率；(2)、若该品牌电动自行车的进价为2300元，售价为2800元，则该经销商1至3月共盈利多少元？17. 如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB．
(1)、若CD=16，BE=4，求⊙O的直径；(2)、若∠M=∠D，求∠D的度数．18. 如图所示，可以自由转动的转盘被3等分，指针落在每个扇形内的机会均等．
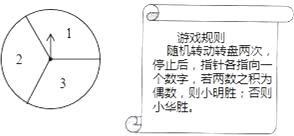(1)、现随机转动转盘一次，停止后，指针指向1的概率是多少；(2)、小明和小华利用这个转盘做游戏，若采用下列游戏规则，你认为对双方公平吗？请用列表或画树状图的方法说明理由．19. 如图，点 在⊙ 的直径 的延长线上，点 在⊙ 上， ， ．
(1)、求证： 是⊙ 的切线；(2)、若⊙ 的半径为 ，求图中阴影部分的面积．
20. 某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现，若每箱以50元的价格调查，平均每天销售90箱，价格每提高1元，平均每天少销售3箱．
(1)、求平均每天销售量y（箱）与销售价x（元/箱）之间的函数关系式．(2)、求该批发商平均每天的销售利润w（元）与销售价x（元/箱）之间的函数关系式．
(3)、当每箱苹果的销售价为多少元时，可以获得最大利润？最大利润是多少？
