北京市东城区2016-2017学年高二下学期理数期末考试试卷
试卷日期:2017-12-28 考试类型:期末考试
一、单选题
-
1. 复数 ,则 在复平面内对应的点所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 直线 ( 为参数)的斜率为( )A、 B、 C、 D、3. 在 的展开式中, 的系数为( )
A、 B、 C、 D、4. 一名老师和四名学生站成一排照相,学生请老师站在正中间,则不同的站法为( )A、4种 B、12种 C、24种 D、120种5. 在极坐标系中,点 到直线 的距离为( )A、 B、 C、 D、6. 袋子中装有大小完全相同的6个红球和4个黑球,从中任取2个球,则所取出的两个球中恰有1个红球的概率为( )A、 B、 C、 D、7. 函数 的图象大致为( )A、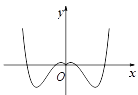 B、
B、 C、
C、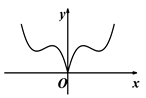 D、
D、 8. 甲、乙两人约好一同去看《变形金刚5》,两人买完了电影票后,偶遇丙也来看这场电影,此时还剩9张该场电影的电影票,电影票的座位信息如下表.
8. 甲、乙两人约好一同去看《变形金刚5》,两人买完了电影票后,偶遇丙也来看这场电影,此时还剩9张该场电影的电影票,电影票的座位信息如下表.1排4号
1排5号
1排8号
2排4号
3排1号
3排5号
4排1号
4排2号
4排8号
丙从这9张电影票中挑选了一张,甲、乙询问丙所选的电影票的座位信息,丙只将排数告诉了甲,只将号数告诉了乙.下面是甲、乙关于丙所选电影票的具体座位信息的一段对话:
甲对乙说:“我不能确定丙的座位信息,你肯定也不能确定.”
乙对甲说:“本来我不能确定,但是现在我能确定了.”
甲对乙说:“哦,那我也能确定了!”
根据上面甲、乙的对话,判断丙选择的电影票是( )
A、4排8号 B、3排1号 C、1排4号 D、1排5号二、填空题
-
9. 是虚数单位,复数 .10. 定积分 的值为 .11. 在高台跳水运动中,某运动员相对于水面的高度 (单位: )与起跳后的时间 (单位: )存在函数关系 .则该运动员在 时的瞬时速度为 .12. 若 ,则 的值为 .13. 随着中国电子商务的发展和人们对网购的逐渐认识,网购鲜花速递行业迅速兴起.佳佳为祝福母亲的生日,准备在网上定制一束混合花束.客服为佳佳提供了两个系列,如下表:
粉色系列
黄色系列
玫 瑰
戴安娜、粉佳人、糖果、桃红雪山
假日公主、金辉、金香玉
康乃馨
粉色、小桃红、白色粉边
火焰、金毛、黄色
配 叶
红竹蕉、情人草、满天星
散尾叶、栀子叶、黄莺、银叶菊
佳佳要在两个系列中选一个系列,再从中选择2种玫瑰、1种康乃馨、2种配叶组成混合花束.请问佳佳可定制的混合花束一共有种.
14. 已知平面向量 ,平面向量 ,(其中 ).定义: .若 , ,则 =;
若 ,且 , ,则 , (写出一组满足此条件的 和 即可).
15. 已知数列 的前 项和为 ,且满足 ,求数列 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.思路1:先设 的值为1,根据已知条件,计算出 , , .
猜想: .
然后用数学归纳法证明.证明过程如下:
①当 时, , 猜想成立
②假设 ( N*)时,猜想成立,即 .
那么,当 时,由已知 ,得 .
又 ,两式相减并化简,得 (用含 的代数式表示).
所以,当 时,猜想也成立.
根据①和②,可知猜想对任何 N*都成立.
思路2:先设 的值为1,根据已知条件,计算出 .
由已知 ,写出 与 的关系式: ,
两式相减,得 与 的递推关系式: .
整理: .
发现:数列 是首项为 , 公比为的等比数列.
得出:数列 的通项公式 , 进而得到 .
三、解答题
-
16. 已知函数 .
(I)求函数 在点 处的切线方程;
(II)求函数 的极值.
17. 电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.表1
观看方式
年龄(岁)
电视
网络
150
250
120
80

求:(I)假设同一组中的每个数据用该组区间的中点值代替,求非常喜欢《人民的名义》这部电视剧的观众的平均年龄;
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
附:
18. 为响应市政府“绿色出行”的号召,王老师每个工作日上下班由自驾车改为选择乘坐地铁或骑共享单车这两种方式中的一种出行.根据王老师从2017年3月到2017年5月的出行情况统计可知,王老师每次出行乘坐地铁的概率是0.4,骑共享单车的概率是0.6.乘坐地铁单程所需的费用是3元,骑共享单车单程所需的费用是1元.记王老师在一个工作日内上下班所花费的总交通费用为X元,假设王老师上下班选择出行方式是相互独立的.(I)求X的分布列和数学期望 ;
(II)已知王老师在2017年6月的所有工作日(按22个工作日计)中共花费交通费用110元,请判断王老师6月份的出行规律是否发生明显变化,并依据以下原则说明理由.
原则:设 表示王老师某月每个工作日出行的平均费用,若 ,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注: )