江苏省扬州市高邮市2017-2018学年高二上学期数学期中考试试卷

试卷日期：2017-12-13 考试类型：期中考试

前去【出卷网】下载

一、填空题

1. 若点A（1，2）在直线ax+3y﹣5=0上，则实数a的值为．

查看试题解析
2. 命题“∃x＜3，x²＞9”的否定是．

查看试题解析
3. 抛物线y= $\frac{x^{2}}{4}$ 的准线方程是．

查看试题解析
4. 命题“若α是钝角，则sinα＞0”的逆否命题为．

查看试题解析
5. 若直线ax+2y+6=0与直线x+（a﹣1）y+2=0垂直，则实数a的值为．

查看试题解析
6. 若命题“∃t∈R，t²﹣a＜0”是真命题，则实数a的取值范围是．

查看试题解析
7. 已知p：0＜m＜1，q：椭圆 $\frac{x^{2}}{m}$ +y²=1的焦点在y轴上，则p是q的条件．（填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”填空）

查看试题解析
8. 若两条直线x+ay+3=0，（a﹣1）x+2y+a+1=0互相平行，则这两条直线之间的距离为．

查看试题解析
9. 若椭圆 $\frac{x^{2}}{16} + \frac{y^{2}}{7} = 1$ 和双曲线 $x^{2} - \frac{y^{2}}{8} = 1$ 有相同的焦点F₁ ， F₂ ，点P是两条曲线的一个交点，则PF₁•PF₂的值是．

查看试题解析
10. 若不等式x²﹣2x+3﹣a＜0成立的一个充分条件是0＜x＜5，则实数a的取值范围是．

查看试题解析
11. 在平面直角坐标系xOy中，已知抛物线y²=8x上一点P到点A（4，0）的距离等于它到准线的距离，则PA= ．

查看试题解析
12. 在△ABC中， $A = \frac{π}{6}$ ，BC=2，D是BC的一个三等分点，则AD的最大值是．

查看试题解析
13. 如图，在平面直角坐标系xOy中，F₁ ， F₂分别是椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）的左、右焦点，B，C分别为椭圆的上、下顶点，直线BF₂与椭圆的另一个交点为D，若 $t a n ∠ F_{1} B O = \frac{1}{2}$ ，则直线CD的斜率为．

查看试题解析
14. 如图，在平面直角坐标系xOy中，F是椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点，直线 $y = \frac{2 b}{3}$ 与椭圆交于B，C两点，且∠BFC=90°，则该椭圆的离心率为．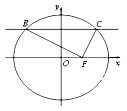

查看试题解析

二、解答题

15. 已知△ABC中，BC边上的高所在的直线方程为x﹣2y+1=0，∠A的平分线所在直线的方程为y=0．

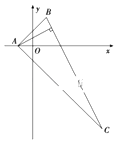(1)、求点A的坐标；

(2)、若点B的坐标为（1，2），求点C的坐标．

查看试题解析
16. 已知p：x²﹣2x﹣8≤0，q：x²+mx﹣6m²≤0，m＞0．

(1)、若q是p的必要不充分条件，求m的取值范围；

(2)、若¬p是¬q的充分不必要条件，求m的取值范围．

查看试题解析
17. 在平面直角坐标系xOy中，已知中心在原点，焦点在x轴上的双曲线C的离心率为 $\sqrt{2}$ ，且双曲线C与斜率为2的直线l相交，且其中一个交点为P（﹣3，0）．

(1)、求双曲线C的方程及它的渐近线方程；

(2)、求以直线l与坐标轴的交点为焦点的抛物线的标准方程．

查看试题解析
18. 已知直线l与圆C：x²+y²+2x﹣4y+a=0相交于A，B两点，弦AB的中点为M（0，1）．

(1)、若圆C的半径为 $\sqrt{3}$ ，求实数a的值；

(2)、若弦AB的长为6，求实数a的值；

(3)、当a=1时，圆O：x²+y²=2与圆C交于M，N两点，求弦MN的长．

查看试题解析
19. 在平面直角坐标系xOy中，已知椭圆C： $\frac{x^{2}}{m + 16} + \frac{y^{2}}{m} = 1$ （m＞0）的离心率为 $\frac{4}{5}$ ，A，B分别为椭圆的左、右顶点，F是其右焦点，P是椭圆C上异于A、B的动点．

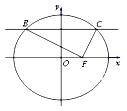(1)、求m的值及椭圆的准线方程；

(2)、设过点B且与x轴的垂直的直线交AP于点D，当直线AP绕点A转动时，试判断以BD为直径的圆与直线PF的位置关系，并加以证明．

查看试题解析
20. 在平面直角坐标系xOy中，已知动圆S过定点P（﹣2 $\sqrt{2} ， 0$ ），且与定圆Q：（x﹣2 $\sqrt{2}$ ）²+y²=36相切，记动圆圆心S的轨迹为曲线C．

(1)、求曲线C的方程；

(2)、设曲线C与x轴，y轴的正半轴分别相交于A，B两点，点M，N为椭圆C上相异的两点，其中点M在第一象限，且直线AM与直线BN的斜率互为相反数，试判断直线MN的斜率是否为定值．如果是定值，求出这个值；如果不是定值，说明理由；

(3)、在（2）条件下，求四边形AMBN面积的取值范围．

查看试题解析