江苏省南京市高淳区2017年中考数学二模试卷

试卷日期：2017-12-13 考试类型：中考模拟

前去【出卷网】下载

一、选择题

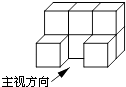
1. $\sqrt{4}$ 的值等于（）

A、2 B、﹣2 C、±2 D、16

查看试题解析
2. 在△ABC中，∠C=90°，BC=3，AC=4，则sinA的值是（）

A、 $\frac{3}{4}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{4}{3}$

查看试题解析
3. 如图是小强用八块相同的小正方体搭建的一个积木，它的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 计算a²•（ $\frac{1}{a}$ ）³的结果是（）

A、a B、a⁵ C、 $\frac{1}{a}$ D、 $\frac{1}{a^{5}}$

查看试题解析
5. 已知反比例函数 $y = \frac{2}{x}$ ，下列结论中，不正确的是（）

A、图象必经过点（1，2） B、y随x的增大而增大 C、图象在第一、三象限内 D、若x＞1，则0＜y＜2

查看试题解析
6. 如图，⊙O的半径为1，△ABC是⊙O的内接等边三角形，点D，E在圆上，四边形BCDE为矩形，这个矩形的面积是（）

A、2 B、 $\frac{3}{2}$ C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析

二、填空题

7. PM 2.5造成的损失巨大，治理的花费更大．我国每年因为空气污染造成的经济损失高达约5659亿元．将5659亿元用科学记数法表示为亿元．

查看试题解析
8. 函数y= $\sqrt{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
9. 分解因式：4x³﹣x= ．

查看试题解析
10. 计算： $\sqrt{8}$ ﹣ $\sqrt{\frac{1}{3}}$ × $\sqrt{6}$ = ．

查看试题解析
11. 在平面直角坐标系中，点A的坐标是（﹣2，3），作点A关于x轴的对称点，得到点A′，再将点A'向右平移3个单位得到点A″，则点A''的坐标是．

查看试题解析
12. 如图，在△ABC中，AB=BC，∠ABC=120°，AB的垂直平分线DE交AC于点D，连接BD，则∠ABD=°．

查看试题解析

13. 某班10名学生校服尺寸与对应人数如下表所示：

尺寸（cm）	160	165	170	175	180
学生人数（人）	1	3	2	2	2

则这10名学生校服尺寸的中位数为cm．

查看试题解析

14. 二次函数y=x²﹣2x+m的图象与x轴的一个交点的坐标是（﹣1，0），则图象与x轴的另一个交点的坐标是．

查看试题解析
15. 如图，点A，B，C在⊙O上，∠ACB的度数是20°， $\hat{A B}$ 的长为π，则⊙O的半径是．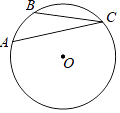

查看试题解析
16. 已知二次函数y=m （x﹣1）（ x﹣4）的图象与x轴交于A，B两点（点A在点B的左边），顶点为C，将该二次函数的图象关于x轴翻折，所得图象的顶点为D．若四边形ACBD为正方形，则m的值为．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{matrix} 2 x + 5 \leq 3 (x + 2) \\ \frac{x - 1}{2} < \frac{x}{3} \end{matrix}$ ，并写出不等式组的整数解．

查看试题解析
18. 先化简，再求值：（ $\frac{1}{a^{2} - 2 a}$ ﹣ $\frac{2}{a^{2} - 4 a + 4}$ ）÷ $\frac{a + 2}{a}$ ，其中a=2+ $\sqrt{2}$ ．

查看试题解析
19. 为增强学生环保意识，某中学组织全校2000名学生参加环保知识大赛，比赛成绩均为整数．从中抽取部分同学的成绩进行统计，并绘制成如图统计图．
请根据图中提供的信息，解答下列问题：

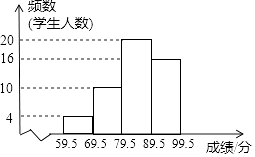(1)、所抽取的样本容量为．

(2)、若抽取的学生成绩用扇形图来描述，则表示“第三组（79.5～89.5 ）”的扇形的圆心角度数为多少？

(3)、如果成绩在80分以上（含80分）的同学可以获奖，请估计该校有多少名同学获奖．

查看试题解析
20. 如图①、②、③是三个可以自由转动的转盘．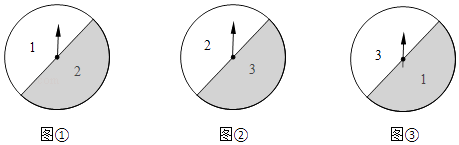

(1)、若同时转动①、②两个转盘，则两个转盘停下时指针所指的数字都是2的概率为；

(2)、甲、乙两人用三个转盘玩游戏，甲转动转盘，乙记录指针停下时所指的数字．游戏规定：当指针所指的三个数字中有数字相同时，就算甲赢，否则就算乙赢．请判断这个游戏是否公平，并说明你的理由．

查看试题解析
21. 人民商场销售某种冰箱，每台进价为2500元，市场调研表明：当每台销售价定为2900元时，平均每天能售出8台；每台售价每降低50元，平均每天能多售出4台．
设该种冰箱每台的销售价降低了x元．

(1)、填表：

每天售出的冰箱台数（台）
每台冰箱的利润（元）
降价前
8
降价后

(2)、若商场要想使这种冰箱的销售利润平均每天达到5000元，则每台冰箱的售价应定为多少元？

查看试题解析
22. 如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上
一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE．

(1)、求证：CE=AD；

(2)、当D在AB中点时．
①求证：四边形BECD是菱形；
②当∠A为多少度时，四边形BECD是正方形？说明理由．

查看试题解析
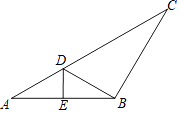
23. 图①为平地上一幢建筑物与铁塔图，图②为其示意图．建筑物AB与铁塔CD都垂直于地面，BD=20m，在A点测得D点的俯角为45°，测得C点的仰角为58°．求铁塔CD的高度．（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）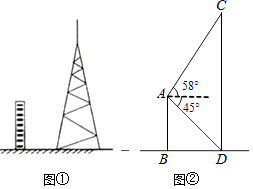

查看试题解析
24. 某市举行“迷你马拉松”长跑比赛，运动员从起点甲地出发，跑到乙地后，沿原路线再跑回点甲地．设该运动员离开起点甲地的路程s（km）与跑步时间t（min）之间的函数关系如图所示．已知该运动员从甲地跑到乙地时的平均速度是0.2km/min，根据图象提供的信息，解答下列问题：

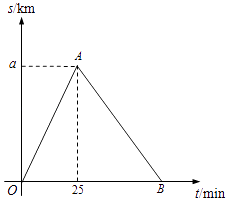(1)、a=km；

(2)、组委会在距离起点甲地3km处设立一个拍摄点P，该运动员从第一次过P点到第二次过P点所用的时间为24min．
①求AB所在直线的函数表达式；
②该运动员跑完全程用时多少min？

查看试题解析
25. 已知二次函数y=﹣x²+2mx﹣2m²﹣3（m为常数）．

(1)、求证：不论m为何值，该二次函数图象与x轴没有公共点；

(2)、如果把该函数图象沿y轴向上平移4个单位后，得到的函数图象与x轴只有一个公共点，试求m的值．

查看试题解析
26. 如图，△ABC中，AB=AC，以AC为直径的⊙O与边AB，BC分别交于点D，E．过E的直线与⊙O相切，与AC的延长线交于点G，与AB交于点F．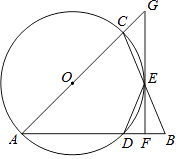

(1)、求证：△BDE为等腰三角形；

(2)、求证：GF⊥AB；

(3)、若⊙O半径为3，DF=1，求CG的长．

查看试题解析
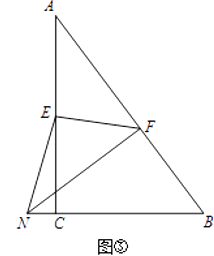
27. 如图，已知一个直角三角形纸片ACB，其中∠ACB=90°，AC=4，BC=3，E，F分别是AC，AB边上点，连接EF，将纸片ACB的一角沿EF折叠．

(1)、如图①，若折叠后点A落在AB边上的点D处，且使S_{四边形ECBF}=3S_△AEF ，则AE=；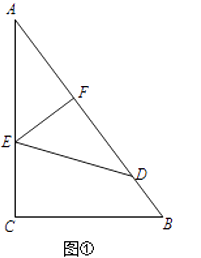

(2)、如图②，若折叠后点A落在BC边上的点M处，且使MF∥CA．求AE的长；

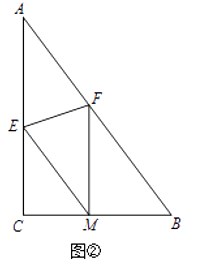(3)、如图③，若折叠后点A落在BC延长线上的点N处，且使NF⊥AB．求AE的长．

查看试题解析

	每天售出的冰箱台数（台）	每台冰箱的利润（元）
降价前	8
降价后