河北省唐山市丰润区2017年中考数学一模试卷

试卷日期：2017-12-13 考试类型：中考模拟

前去【出卷网】下载

一、选择题

1. 计算： $\sqrt{9}$ =（）

A、5 B、2 C、4 D、3

查看试题解析
2. 小明从正面观察如图所示的两个物体，看到的大致图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算错误的是（）

A、3 $\sqrt{3} - \sqrt{3}$ =2 $\sqrt{3}$ B、﹣2+|﹣2|=0 C、x²•x³=x⁶ D、（﹣3）²=9

查看试题解析
4. 把多项式x²﹣6x+9分解因式，结果正确的是（）

A、（x﹣3）² B、（x﹣9）² C、（x+3）（x﹣3） D、（x+9）（x﹣9）

查看试题解析
5. 如图，直线AB∥CD，AE平分∠CAB，AE与CD相交于点E，∠ACD=40°，则∠DEA=（）

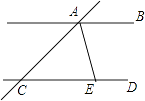A、40° B、110° C、70° D、140°

查看试题解析
6. 一种病毒的直径约为0.000043m，0.000043m用科学记数法表示为（）

A、4.3×10^﹣⁴m B、4.3×10^﹣⁵m C、43×10^﹣⁵m D、0.43×10^﹣⁴m

查看试题解析
7. 如图，在▱ABCD中，对角线AC与BD交于点O，若增加一个条件，使▱ABCD成为菱形，下列给出的条件不正确的是（）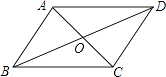

A、AB=AD B、AC⊥BD C、AC=BD D、∠BAC=∠DAC

查看试题解析
8. 若关于x的方程x²﹣2 $\sqrt{3}$ x﹣k=0有两个相等的实数根，则k的值为（）

A、﹣1 B、0 C、﹣3 D、﹣ $\frac{3}{2}$

查看试题解析
9. 如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（﹣3，2），（b，m），（c，m），则点E的坐标是（）

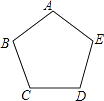A、（2，﹣3） B、（2，3） C、（3，2） D、（3，﹣2）

查看试题解析
10. 如图，在△ABC中，BF平分∠ABC，AF⊥BF于点F，D为AB的中点，连接DF延长交AC于点E．若AB=10，BC=16，则线段EF的长为（）

A、2 B、3 C、4 D、5

查看试题解析
11. 如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则此时轮船所在位置B处与灯塔P之间的距离为（）

A、60海里 B、45海里 C、20 $\sqrt{3}$ 海里 D、30 $\sqrt{3}$ 海里

查看试题解析
12. 如图．⊙O的直径AB垂直弦CD于E点，∠A=22.5°，OC=4，CD的长为（）

A、4 B、8 C、2 $\sqrt{2}$ D、4 $\sqrt{2}$

查看试题解析
13. 如图，在3×3的方格中，A，B，C，D，E，F分别位于格点上，从C，D，E，F四点中任意取一点，与点A，B为顶点作三角形，则所作三角形为等腰三角形的概率是（）

A、1 B、 $\frac{1}{4}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
14. 若x²+4x﹣4=0，则3（x﹣2）²﹣6（x+1）（x﹣1）的值为（）

A、﹣6 B、6 C、18 D、30

查看试题解析
15. 如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S₁、S₂、S₃；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S₄、S₅、S₆ ．其中S₁=16，S₂=45，S₅=11，S₆=14，则S₃+S₄=（）

A、86 B、64 C、54 D、48

查看试题解析
16. 如图，已知：如图，在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线y= $\frac{k}{x}$ （x＞0）经过D点，交BC的延长线于E点，且OB•AC=160，有下列四个结论：
①双曲线的解析式为y= $\frac{40}{x}$ （x＞0）；②E点的坐标是（5，8）；③sin∠COA= $\frac{4}{5}$ ；④AC+OB=12 $\sqrt{5}$ ．其中正确的结论有（）

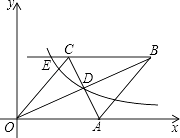A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

17. 计算：﹣2×3= ．

查看试题解析
18. 如图，⊙O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是．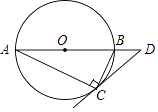

查看试题解析
19. 如图，将一张等边三角形纸片沿中位线剪成4个小三角形，称为第一次操作：然后，将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；…根据以上操作，①第七次操作共得到个三角形；②若要得到220个小三角形，则需要操作的次数是．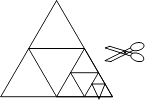

查看试题解析

三、解答题

20. 计算题

(1)、计算：（﹣ $\frac{1}{2}$ ）^﹣²﹣| $\sqrt{3}$ ﹣1|+（﹣ $\sqrt{3}$ +1）⁰+3tan30°

(2)、解方程： $\frac{x}{x - 1}$ + $\frac{2}{1 - x}$ =4．

查看试题解析
21. 已知：如图△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．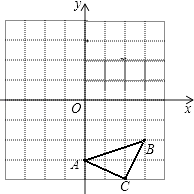

①画出△ABC向上平移6个单位得到的△A₁B₁C₁；

②以点C为位似中心，在网格中画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且△A₂B₂C₂与△ABC的位似比为2：1，并直接写出点A₂的坐标．

查看试题解析
22. 某校对七、八、九年级的学生进行体育水平测试，成绩评定为优秀、良好、合格、不合格四个等第．为了解这次测试情况，学校从三个年级随机抽取200名学生的体育成绩进行统计分析．相关数据的统计图、表如下：
各年级学生成绩统计表

优秀
良好
合格
不合格
七年级
a
20
24
8
八年级
29
13
13
5
九年级
24
b
14
7
根据以上信息解决下列问题：

(1)、在统计表中，a的值为， b的值为；

(2)、在扇形统计图中，八年级所对应的扇形圆心角为度；

(3)、若该校三个年级共有2000名学生参加考试，试估计该校学生体育成绩不合格的人数．

查看试题解析
23. 如图，△ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交CE的延长线于F，且AF=BD，连结BF．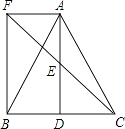

(1)、求证：①△EAF≌△EDC；
②D是BC的中点；

(2)、若AB=AC，求证：四边形AFBD是矩形．

查看试题解析
24. 甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示．

(1)、求甲车从A地到达B地的行驶时间；

(2)、求甲车返回时y与x之间的函数关系式，并写出自变量x的取值范围；

(3)、求乙车到达A地时甲车距A地的路程．

查看试题解析
25. 如图1，△ABC中，∠BAC=90°，AB=AC，四边形ADEF是正方形，点B，C分别在AD，AF上，此时BD=CF，BD⊥CF成立．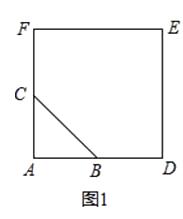

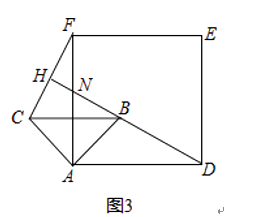
(1)、当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明，若不成立，请说明理由；

(2)、当△ABC绕点A逆时针旋转45°时，如图3，延长DB交AF，CF于点N，H．
①求证：BD⊥CF；
②当AB=2，AD=3 $\sqrt{2}$ 时，求线段AN的长．

查看试题解析
26. 如图，抛物线y=﹣x²+bx+c交x轴于点A（﹣3，0）和点B，交y轴于点C（0，3）．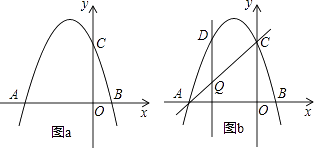

(1)、求抛物线的函数表达式；

(2)、若点P在抛物线上，且S_△_AOP=4S_△_BOC ，求点P的坐标；

(3)、如图b，设点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ长度的最大值．

查看试题解析

各年级学生成绩统计表
	优秀	良好	合格	不合格
七年级	a	20	24	8
八年级	29	13	13	5
九年级	24	b	14	7