江苏省苏州市常熟市2017-2018学年高二上学期数学期中考试试卷
试卷日期：2017-12-12 考试类型：期中考试
一、填空题
-
1. 已知直线l的斜率为﹣1，则它的倾斜角为 ．2. 已知圆C的方程为x2+y2+2x﹣y=0，则它的圆心坐标为 ．3. 若直线a和平面α平行，且直线b⊂α，则两直线a和b的位置关系为 ．4. 已知直线l1：ax+3y﹣1=0与直线l2：2x+（a﹣1）y+1=0垂直，则实数a=5. 已知直线l：x+2y﹣4=0与坐标轴交于A、B两点，O为坐标原点，则经过O、A、B三点的圆的标准方程为 ．6. 圆锥的侧面展开图是半径为3，圆心角为 的扇形，则这个圆锥的高是 ．7. 已知P，Q分别为直线x+3y﹣9=0和x+3y+1=0上的动点，则PQ的最小值为 ．8. 已知m，n是空间两条不同的直线，α，β是两个不同的平面，下面说法正确的有 ．
①若m⊂α，m⊥β，则α⊥β；
②若m⊂α，α∩β=n，α⊥β，则m⊥n；
③若m⊂α，n⊂β，α∥β，则m∥n；
④若m∥α，m⊂β，α∩β=n，则m∥n．
9. 直线x﹣2y+1=0关于直线x=1对称的直线方程是 ．10. 已知底面边长为1，侧棱长为 的正四棱柱，其各顶点均在同一个球面上，则该球的体积为 ．11. 若直线l1：y=x+a和l2：y=x+b将圆（x﹣1）2+（y﹣2）2=8分成长度相同的四段弧，则ab= ．12. 已知正三棱锥的体积为9 cm3 ， 高为3cm．则它的侧面积为 cm2 ．13. 已知点A（1，2），B（﹣3，﹣1），若圆x2+y2=r2（r＞0）上恰有两点M，N，使得△MAB和△NAB的面积均为5，则r的取值范围是 ．14. 已知线段AB的长为2，动点C满足 （μ为常数，μ＞﹣1），且点C始终不在以点B为圆心 为半径的圆内，则μ的范围是 ．二、解答题
-
15. 如图：四棱锥P﹣ABCD中，PD=PC，底面ABCD是直角梯形AB⊥BC，AB∥CD，CD=2AB，点M是CD的中点．
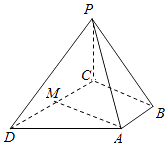(1)、求证：AM∥平面PBC；(2)、求证：CD⊥PA．16. 已知平行四边形ABCD的三个顶点的坐标为A（﹣1，5），B（﹣2，﹣1），C（2，3）．
(1)、求平行四边形ABCD的顶点D的坐标；(2)、在△ACD中，求CD边上的高所在直线方程；(3)、求四边形ABCD的面积．17. 已知圆C经过A（﹣2，1），B（5，0）两点，且圆心C在直线y=2x上．(1)、求圆C的方程；(2)、动直线l：（m+2）x+（2m+1）y﹣7m﹣8=0过定点M，斜率为1的直线m过点M，直线m和圆C相交于P，Q两点，求PQ的长度．
18. 斜棱柱ABC﹣A1B1C1中，侧面AA1C1C⊥面ABC，侧面AA1C1C为菱形，∠A1AC=60°，E，F分别为A1C1和AB的中点．
(1)、求证：平面CEF⊥平面ABC；
(2)、若三棱柱的所有棱长为2，求三棱柱F﹣ECB的体积；(3)、D为棱BC上一点，若C1D∥EF，请确定点D位置，并证明你的结论．