江苏省淮安市、宿迁市2017-2018学年高三上学期数学期中考试试卷

试卷日期：2017-12-12 考试类型：期中考试

前去【出卷网】下载

一、填空题

1. 已知集合A={x|0＜x＜2}，B={x|﹣1＜x＜1}，则A∩B= ．

查看试题解析
2. 复数z=i（1﹣2i）（i是虚数单位）的实部为．

查看试题解析
3. 函数y=log₂（3x﹣1）的定义域是．

查看试题解析
4. 某校高三年级500名学生中，血型为O型的有200人，A型的有125人，B型的有125人，AB型的有50人．为研究血型与色弱之间的关系，现用分层抽样的方法从这500名学生中抽取一个容量为60的样本，则应抽取名血型为AB的学生．

查看试题解析
5. 如图是一个算法流程图，则输出的i的值为．

查看试题解析
6. 连续抛一枚均匀的硬币3次，恰好2次正面向上的概率为．

查看试题解析
7. 已知 $s i n α = c o s \frac{2 π}{5}$ ，0＜α＜π，则α的取值集合为．

查看试题解析
8. 在平行四边形ABCD中，AB=2，AD=1，∠ABC=60°，则 $\vec{A B} \cdot \vec{A C}$ 的值为．

查看试题解析
9. 设等差数列{a_n}的前n项和为S_n ．若a₃=5，且S₁ ， S₅ ， S₇成等差数列，则数列{a_n}的通项公式a_n= ．

查看试题解析
10. 在平面直角坐标系xOy中，已知点A（﹣1，0），B（1，0）均在圆C：（x﹣3）²+（y﹣4）²=r²外，且圆C上存在唯一一点P满足AP⊥BP，则半径r的值为．

查看试题解析
11. 已知函数f（x）=x³ ．设曲线y=f（x）在点P（x₁ ， f（x₁））处的切线与该曲线交于另一点Q（x₂ ， f（x₂）），记f'（x）为函数f（x）的导数，则 $\frac{f' (x_{1})}{f' (x_{2})}$ 的值为．

查看试题解析
12. 已知函数f（x）与g（x）的图象关于原点对称，且它们的图象拼成如图所示的“Z”形折线段ABOCD，不含A（0，1），B（1，1），O（0，0），C（﹣1，﹣1），D（0，﹣1）五个点．则满足题意的函数f（x）的一个解析式为．

查看试题解析
13. 不等式x⁶﹣（x+2）³+x²≤x⁴﹣（x+2）²+x+2的解集为．

查看试题解析
14. 在锐角三角形ABC中，9tanAtanB+tanBtanC+tanCtanA的最小值为．

查看试题解析

二、解答题

15. 如图，在直三棱柱ABC﹣A₁B₁C₁中，AC=BC，点M为棱A₁B₁的中点．
求证：

(1)、AB∥平面A₁B₁C；

(2)、平面C₁CM⊥平面A₁B₁C．

查看试题解析
16. 设△ABC的内角A，B，C所对边分别为a，b，c．向量 $\vec{m}$ =（a， $\sqrt{3}$ b）， $\vec{n}$ =（sinB，﹣cosA），且 $\vec{m}$ ⊥ $\vec{n}$ ．

(1)、求A的大小；

(2)、若| $\vec{n}$ |= $\frac{\sqrt{6}}{4}$ ，求cosC的值．

查看试题解析
17. 如图，在平面直角坐标系xOy中，过椭圆C： $\frac{x^{2}}{4} + y^{2} = 1$ 的左顶点A作直线l，与椭圆C和y轴正半轴分别交于点P，Q．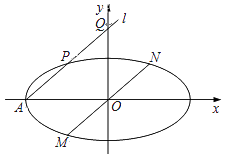

(1)、若AP=PQ，求直线l的斜率；

(2)、过原点O作直线l的平行线，与椭圆C交于点M，N，求证： $\frac{A P \cdot A Q}{M N^{2}}$ 为定值．

查看试题解析
18. 将2张边长均为1分米的正方形纸片分别按甲、乙两种方式剪裁并废弃阴影部分．

(1)、在图甲的方式下，剩余部分恰能完全覆盖某圆锥的表面，求该圆锥的母线长及底面半径；

(2)、在图乙的方式下，剩余部分能完全覆盖一个长方体的表面，求长方体体积的最大值．

查看试题解析
19. 对于给定的正整数k，如果各项均为正数的数列{a_n}满足：对任意正整数n（n＞k），a_n_﹣ka_n_﹣k+1…a_n_﹣1a_n+1…a_n+k_﹣1a_n+k=a_n^2k总成立，那么称{a_n}是“Q（k）数列”．

(1)、若{a_n}是各项均为正数的等比数列，判断{a_n}是否为“Q（2）数列”，并说明理由；

(2)、若{a_n}既是“Q（2）数列”，又是“Q（3）数列”，求证：{a_n}是等比数列．

查看试题解析
20. 设命题p：对任意的 $x \in [0 ， \frac{π}{2})$ ，sinx≤ax+b≤tanx恒成立，其中a，b∈R．

(1)、若a=1，b=0，求证：命题p为真命题．

(2)、若命题p为真命题，求a，b的所有值．

查看试题解析
21. 在△ABC中，AB=AC，△ABC的外接圆⊙O的弦AD的延长线交BC的延长线于点E．
求证：△ABD∽△AEB．

查看试题解析
22. 已知变换T把直角坐标平面上的点A（3，﹣4），B（0，5）分别变换成点A'（2，﹣1），B'（﹣1，2），求变换T对应的矩阵M．

查看试题解析
23. 在极坐标系中，已知直线 $ρ c o s (θ + \frac{π}{3}) = 2$ 与圆ρ=acosθ（a＞0）相切，求a的值．

查看试题解析
24. 已知正数x，y，z满足x+y+z=4，求 $\frac{x^{2}}{4} + \frac{y^{2}}{9} + z^{2}$ 的最小值．

查看试题解析
25. 小明设置的手机开机密码若连续3次输入错误，则手机被锁定，5分钟后，方可重新输入．某日，小明忘记了开机密码，但可以确定正确的密码是他常用的4个密码之一，于是，他决定逐个（不重复）进行尝试．

(1)、求手机被锁定的概率；

(2)、设第X次输入后能成功开机，求X的分布列和数学期望E（X）．

查看试题解析
26. 设n≥3，n∈N^* ，在集合{1，2，…，n}的所有元素个数为2的子集中，把每个子集的较大元素相加，和记为a，较小元素之和记为b．

(1)、当n=3时，求a，b的值；

(2)、求证：对任意的n≥3，n∈N^* ， $\frac{b}{a}$ 为定值．

查看试题解析