【基础练】人教版数学八年级下学期 18.2.2 菱形
试卷日期:2025-05-14 考试类型:单元试卷
一、选择题
-
1. 已知四边形中,对角线与相交于点O, , 下列判断错误的是( )A、如果 , , 那么四边形是矩形 B、如果 , , 那么四边形是矩形 C、如果 , , 那么四边形是菱形 D、如果 , , 那么四边形是菱形2. 下列平行四边形中,根据图中所标出的数据,不一定是菱形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 用直尺和圆规在一个矩形内作菱形 , 下列作法中, 错误的是( )A、
3. 用直尺和圆规在一个矩形内作菱形 , 下列作法中, 错误的是( )A、 B、
B、 C、
C、 D、
D、 4. 菱形具有而矩形不一定具有的性质是( )A、对角相等 B、邻角互补 C、对角线互相平分 D、对角线平分一组对角5. 分别为矩形ABCD四边的中点,则四边形一定是( )A、矩形 B、菱形 C、正方形 D、非特殊的平行四边形6. 如图,在菱形ABCD中,AC=8,菱形ABCD的面积为24,则其周长为( )
4. 菱形具有而矩形不一定具有的性质是( )A、对角相等 B、邻角互补 C、对角线互相平分 D、对角线平分一组对角5. 分别为矩形ABCD四边的中点,则四边形一定是( )A、矩形 B、菱形 C、正方形 D、非特殊的平行四边形6. 如图,在菱形ABCD中,AC=8,菱形ABCD的面积为24,则其周长为( ) A、20 B、24 C、28 D、407. 如图,菱形的顶点坐标为 , 顶点的坐标为( )
A、20 B、24 C、28 D、407. 如图,菱形的顶点坐标为 , 顶点的坐标为( ) A、 B、 C、 D、8. 如图,矩形的对角线 , 相交于点O , , , 点M , N分别是 , 的中点,连接 , 若四边形的周长是16,则的长为( )
A、 B、 C、 D、8. 如图,矩形的对角线 , 相交于点O , , , 点M , N分别是 , 的中点,连接 , 若四边形的周长是16,则的长为( ) A、1 B、2 C、4 D、89. 如图,四边形是菱形,过点的直线分别交 , 的延长线于点 , , 若 , , 则等于( )
A、1 B、2 C、4 D、89. 如图,四边形是菱形,过点的直线分别交 , 的延长线于点 , , 若 , , 则等于( )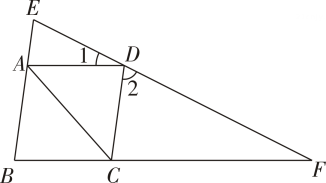 A、 B、 C、 D、10. 如图,菱形的两条对角线交于点 , 于点 , 若 , , 则的长是( )
A、 B、 C、 D、10. 如图,菱形的两条对角线交于点 , 于点 , 若 , , 则的长是( ) A、 B、 . C、 D、411. 如图,在菱形ABCD中,E、F分别是边CD、BC上的动点,连接AE , EF , G、H分别为AE、EF的中点,连接GH . 若∠D=45°,AD=4,则GH的最小值为( )
A、 B、 . C、 D、411. 如图,在菱形ABCD中,E、F分别是边CD、BC上的动点,连接AE , EF , G、H分别为AE、EF的中点,连接GH . 若∠D=45°,AD=4,则GH的最小值为( ) A、2 B、4 C、 D、
A、2 B、4 C、 D、二、填空题
-
12. 菱形的两条对角线的长分别为6和8,则这个菱形的周长为.13. 如图,在菱形中, , 则的长为 .
 14. 如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 , 使ABCD成为菱形(只需添加一个即可)
14. 如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 , 使ABCD成为菱形(只需添加一个即可) 15. 如图,菱形中, , , 交于点O,若E是边的中点, , 则的长等于 , 的度数为 .
15. 如图,菱形中, , , 交于点O,若E是边的中点, , 则的长等于 , 的度数为 . 16. 某校的校门是伸缩门(图①).整个伸缩门在每个横向位置上都有30个连在一起的菱形结构,每个菱形结构的边长都是 . 若校门完全关闭时,每个菱形结构的锐角都是(图②).当校门部分打开时,每个菱形结构的角都变为角(图③),则此时校门打开的宽度为 .
16. 某校的校门是伸缩门(图①).整个伸缩门在每个横向位置上都有30个连在一起的菱形结构,每个菱形结构的边长都是 . 若校门完全关闭时,每个菱形结构的锐角都是(图②).当校门部分打开时,每个菱形结构的角都变为角(图③),则此时校门打开的宽度为 . 17. 如图,在边长为10的菱形ABCD中,对角线 , 若点是线段BD上的动点,于 , 于.则.
17. 如图,在边长为10的菱形ABCD中,对角线 , 若点是线段BD上的动点,于 , 于.则.
三、解答题
-
18. 如图,在矩形中,O为的中点,过点O作分别交 , 于点E,F.求证:四边形是菱形.
 19. 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
19. 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
 20. 如图,在菱形中,为边的中点,点在边上, , 交的延长线于点 .
20. 如图,在菱形中,为边的中点,点在边上, , 交的延长线于点 . (1)、求证: .(2)、若 , , 则的长为________.
(1)、求证: .(2)、若 , , 则的长为________.


