湘教版（2025)数学七年级下册第五章轴对称与旋转单元测试（培优卷）

试卷日期：2025-04-20 考试类型：单元试卷

前去【出卷网】下载

一、选择题：本题共10小题，每小题3分，共30分

1. 全民阅读有助于提升一个国家、一个民族的精神力量，图书馆是开展全民阅读的重要场所．以下图书馆标志中，其文字上方的图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 以下深圳四家企业标识图案中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 围棋是中华民族发明的迄今最久远、最复杂的智力博弈活动之一，下列围棋图案中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. 在当地时间 $7$ 月 $27$ 日结束的巴黎奥运会 $10$ 米气步枪混合团体比赛中，中国选手黄雨婷/盛李豪夺得本届奥运会首枚金牌，右图是巴黎奥运会射击项目图标，这个图案的对称轴条数为（）

A、 $6$ B、 $4$ C、 $2$ D、 $1$

查看试题解析
5. 如图，在 $3 \times 4$ 的正方形网格中已有 2 个正方形涂黑，再选择一个正方形涂黑，使得 3 个涂黑的正方形组成轴对称图形，选择的位置共有（）

A、7 处 B、4 处 C、3 处 D、2 处

查看试题解析
6. 下列语句中正确的有几个（）
①关于一条直线对称的两个图形一定能重合；②两个能重合的图形一定关于某条直线对称；③两个轴对称图形的对应点一定在对称轴的两侧；④一个圆有无数条对称轴．

A、1 B、2 C、3 D、4

查看试题解析
7. 如图 4×4 的正方形网格中，其中一个三角形①绕某点旋转一定的角度，得到三角形②，则其旋转中心是（）

A、点 A B、点 B C、点 C D、点 D

查看试题解析
8. 如图，在图形T上补上一个正方形，不能使它成为一个轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，将△AOB绕点O按顺时针方向旋转45°后得到△COD，若∠AOB=27°，则∠BOC的度数是(　　)

A、18° B、27° C、45° D、72°

查看试题解析
10. 如图，一块含 $30 °$ 角的直角三角板 $A C B$ 绕点 $C$ 逆时针旋转一定的角度到 $△ A^{'} C B^{'}$ 的位置，且 $A^{'} C ⊥ A B$ ，则三角板 $A B C$ 旋转的角度是（）

A、 $30 °$ B、 $60 °$ C、 $90 °$ D、 $120 °$

查看试题解析

二、填空题：本题共8小题，每小题3分，共24分

11. 如图，在6×6的正方形网格中，选取13个格点，以其中的三个格点A、B、C为顶点画 $△ A B C$ ．若在图中以选取的格点为顶点再画出一个 $△ A B P$ ，使 $△ A B P$ 与 $△ A B C$ 成轴对称，这样的点P有个．

查看试题解析
12. 围棋起源于中国，古代称为“弈”.如图是两位同学的部分对弈图，轮到白方落子，观察棋盘，白方如果落子于点的位置，则所得的对弈图是轴对称图形.(填写 $A, B, C, D$ 中的一处即可， $A, B, C, D$ 位于棋盘的格点上)

查看试题解析
13. 在镜子里看见的时间是，实际时间是．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ，如果将 $△ A B C$ 绕点A顺时针旋转得到 $△ A D E$ ，点D、E分别与点B、C对应，如果 $∠ D A C : ∠ E A C = 1 : 3$ ，那么旋转角（大于 $0 °$ 且小于 $180 °$ ）的大小为 $°$ ．

查看试题解析
15. 如图，先把 $∠ A P B$ 放置在量角器上，读得射线PA、PB分别经过刻度120和144，再把 $∠ A P B$ 绕点 $P$ 逆时针方向旋转到 $∠ A^{^{'}} P B^{^{'}}, ∠ A P B$ 的角平分线PC相应地旋转到 $P C^{^{'}}$ ，读得 $P C^{^{'}}$ 经过刻度52，则 $∠ A' P A$ 的角平分线经过的刻度为.

查看试题解析
16. 一副直角三角尺叠放如图1所示，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动（旋转角不超过180度），使两块三角尺至少有一组边互相平行.如图2：当∠BAD＝15°时，BC∥DE.则∠BAD（0°＜∠BAD＜180°）其它所有可能符合条件的度数为.

查看试题解析
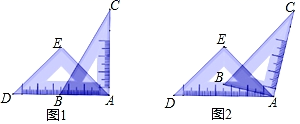17. 一副三角板按如图所示叠放在一起，其中点 $B$ ， $D$ 重合，若固定三角板 $A O B$ ，将三角板 $A C D$ 绕着公共顶点 $A$ ，按逆时针方向旋转 $α$ 度（ $90 < α < 180$ ），当旋转后的 $C D$ 与三角板 $A O B$ 的某一边平行时， $α$ 的值为．

查看试题解析
18. 如图，在直角三角形 $A B C$ 中， $∠ C = 90 °$ ，点D在 $A B$ 上，点G在 $B C$ 上， $△ B D G$ 与 $△ F D G$ 关于直线 $D G$ 对称， $D F$ 与 $B$ 交于点E，若 $D F ∥ A C$ ， $∠ B = 28 °$ ，则 $∠ D G C$ 的度数是度．

查看试题解析

三、解答题：本题共8小题，共66分

19. 如图1，在 $3 \times 3$ 的网格中， $△ A B C$ 三个顶点均在格点上，这样的三角形叫做“格点三角形”．在图中画出一个“格点三角形”（阴影部分）与原 $△ A B C$ 关于某条直线成轴对称．请在图2、图3、图4中，各画一个和原三角形成轴对称的“格点三角形”，并将所画的“格点三角形”用“斜线”涂成“阴影部分”（图 $1 -$ 图4不重复）．

查看试题解析
20. 在 $3 \times 3$ 的正方形格点图中，有格点 $△ A B C$ 和 $△ D E F$ ，且 $△ A B C$ 和 $△ D E F$ 关于某直线成轴对称，请在如图给出的图中画出4个这样的 $△ D E F$ .（每个 $3 \times 3$ 正方形个点图中限画一种，若两个图形中的对称轴是重合的，则视为一种）

查看试题解析
21. 在数学活动课上，王老师要求学生将图1所示的3×3正方形方格纸，剪掉其中两个方格，使之成为轴对称图形．规定：凡通过旋转能重合的图形视为同一种图形，如图2的四幅图就视为同一种设计方案（阴影部分为要剪掉部分）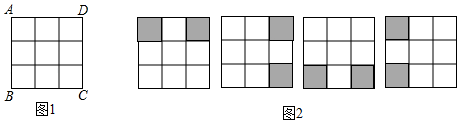

请在图中画出4种不同的设计方案，将每种方案中要剪掉的两个方格涂黑（每个3×3的正方形方格画一种，例图除外）

查看试题解析
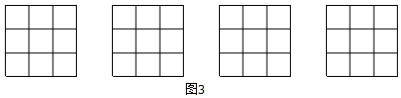22. 如图，在平面直角坐标系中， $Δ A B C$ 的顶点都在正方形网格的格点上，且 $A (4,4), B (3,2), C (1,2)$ .

(1)、在图中画出将 $Δ A B C$ 沿 $x$ 轴向左平移6个单位后得到的 $Δ A_{1} B_{1} C_{1}$ (点 $A$ 、 $B$ 、 $C$ 的对应点分别为点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ )；

(2)、在图中画出将 $Δ A B C$ 绕原点 $O$ 顺时针旋转 $90 °$ 后得到的 $Δ A_{2} B_{2} C_{2}$ (点 $A$ 、 $B$ 、 $C$ 的对应点分别为点 $A_{2}, B_{2}, C_{2})$ .

查看试题解析
23. 如图，在方格纸中，每个小方格的边长均为 $1$ 个单位长度，线段 $A B$ 的两个端点和点 $P$ 都在小方格的格点上．请根据下列要求用无刻度直尺作图．

(1)、将线段 $A B$ 平移，使平移后的线段 $m$ 经过点 $P$ ．
①请在图中画出一条符合要求的线段 $m$ ；
②写出线段 $A B$ 平移至线段 $m$ 的方法；

(2)、第（1）问的线段 $m$ 也可由线段 $A B$ 旋转得到，请作出其旋转中心 $O$ ．

查看试题解析
24. 阅读下面材料：
如图 $1$ ，把 $△ A B C$ 沿直线 $B C$ 平行移动线段 $B C$ 的长度，可以变到 $△ E C D$ 的位置．
如图 $2$ ，以 $B C$ 为轴把 $△ A B C$ 翻折 $180 °$ ，可以变到 $△ D B C$ 的位置．
如图 $3$ ，以A点为中心，把 $△ A B C$ 旋转 $90 °$ ，可以变到 $△ A E D$ 的位置，像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状和大小的图形变换，叫做三角形的全等变换．
如图 $4$ ，在正方形 $A B C D$ 中， $E$ 是 $A D$ 的中点， $F$ 是 $B A$ 延长线上一点， $A F = \frac{1}{2} A B$ ．
回答下列问题

(1)、在如图 $4$ 所示，可以通过平行移动、翻折、旋转中的哪一种方法，使 $△ A B E$ 移到 $△ A D F$ 的位置？

(2)、指出如图 $4$ 所示中的线段 $B E$ 与 $D F$ 之间的关系．

查看试题解析
25. 如图①，直角三角尺 $A B C$ 和直角三角尺 $A D E$ 的顶点 $A$ 重合，且顶点 $C, A, E$ 在一条直线上， $∠ C = ∠ E = 90^{\circ}, ∠ B A C = 60^{\circ}, ∠ D A E = 45^{\circ}$ ，保持三角尺 $A D E$ 不动，将三角尺 $A B C$ 绕顶点 $A$ 顺时针旋转，点 $C$ 落在射线 $A E$ 上时停止旋转．

(1)、如图②，当三角尺 $A B C$ 绕顶点 $A$ 顺时针旋转 $40^{\circ}$ 时，则 $∠ C A D =$ ° $∠ B A E =$ 。

(2)、如图③，当三角尺 $A B C$ 顺时针旋转任意角度 $α^{\circ}$ ，且 $A B$ 在 $A E$ 上方时， $∠ C A D$ 与 $∠ B A E$ 大小之间有何数量关系？并说明理由．

(3)、如图④，若三角尺 $A B C$ 的旋转速度为 $5^{\circ}$ 秒，当 $A B$ 在 $A E$ 下方时，那么多少秒后 $∠ B A E$ 是 $∠ C A D$ 的两倍．

查看试题解析
26. 综合与实践
问题情境：
在数学实践课上，给出两个大小形状完全相同的含有 $30 °$ ， $60 °$ 的直角三角板如图1放置， $P A ， P B$ 在直线 $M N$ 上，且三角板 $P A C$ 和三角板 $P B D$ 均可以点P为顶点运动．

(1)、操作探究：
如图2，若三角板 $P B D$ 保持不动，三角板 $P A C$ 绕点P逆时针旋转一定角度， $P F$ 平分 $∠ A P D ， P E$ 平分 $∠ C P D$ ，求 $∠ E P F$ ；

(2)、如图3，在图1基础上，若三角板 $P A C$ 开始绕点P以每秒 $5 °$ 的速度逆时针旋转，同时三角板 $P B D$ 绕点P以每秒 $1 °$ 的速度逆时针旋转，当 $P A$ 转到与 $P M$ 重合时，两三角板都停止转动．在旋转过程中，当 $P C 、 P B 、 P D$ 三条射线中的其中一条射线平分另两条射线的夹角时，请求出旋转的时间；

(3)、拓广探究：
如图4，作三角板 $P B D$ 关于直线 $P D$ 的对称图形 $P B_{1} D$ ．三角板 $P B D$ 保持不动，三角板 $P A C$ 绕点P逆时针旋转，当 $A C ∥ B_{1} P$ 时，请直接写出旋转角的度数．

查看试题解析

湘教版（2025)数学七年级下册第五章 轴对称与旋转 单元测试（培优卷）

一、选择题：本题共10小题，每小题3分，共30分

二、填空题：本题共8小题，每小题3分，共24分

三、解答题：本题共8小题，共66分

湘教版（2025)数学七年级下册第五章轴对称与旋转单元测试（培优卷）