湘教版（2025)数学七年级下册第五章 轴对称与旋转 单元测试（基础卷）
试卷日期：2025-04-20 考试类型：单元试卷
一、选择题：本题共10小题，每小题3分，共30分
-
1. 下列图标是节水、节能、低碳和绿色食品的标志，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列关于轴对称性质的说法中，错误的是（ ）A、对应线段互相平行 B、对应线段相等 C、对应角相等 D、对应点连线与对称轴垂直3. 正方形有（ ）条对称轴．A、1 B、2 C、4 D、无数4. 围棋是一种棋类游戏，属于琴棋书画四艺之一，其起源于中国，古代称之为“弈”，至今已有四千多年的历史.下列由黑白棋子摆成的图案是轴对称图形的是（ ）A、
B、
C、
D、
5. 如图，绕点P逆时针旋转一个角度得到 ， 则下面选项中不能表示旋转角的是（ ）
A、 B、 C、 D、6. 在绿色食品、回收、节能、节水四个标志中，是由某个基本图形经过旋转得到的是（ ）A、
B、
C、
D、
7. 下列四个图案中，可用平移来分析整个图案的形成过程的图案是( )A、
B、
C、
D、
8. 下面四个图案中，不能由基本图案旋转得到的是（ ）A、
B、
C、
D、
9. 如图， 绕点 顺时针旋转 得到 ， 若 ， 则 的度数是（ ）
A、 B、 C、 D、10. 在图中，将方格纸中的图形绕O点顺时针旋转90°得到的图形是（ ）
A、
B、
C、
D、
二、填空题：本题共8小题，每小题3分，共24分
-
11. 如图是的对称轴， ， ， 则的周长为 ．
12. 我国传统木结构房屋，窗户常用各种图案装饰，下图是一种常见的图案，这个图案有条对称轴．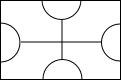
13. 在数字0、2、4、6、8中是轴对称图形的是；14. 如图，将绕点O按逆时针方向旋转40°后得到 ， 若 ， 则的度数是 ．
15. 如图，一个五角星图案，绕着它的中心O旋转，则旋转角至少为时，旋转后的五角星与自身重合．
16. 如图， ， 将绕点O逆时针旋转得到 ， 则的度数为 ．
17. 如图，由个相同的正方形组成的十字形纸片沿直线和剪开后重组可得到矩形 ， 那么②可看作①通过一次得到（填“平移”“旋转”或“轴对称”）．
18. 如图，正三角形网格中，已有两个小正三角形被涂黑，再将图中其余小正三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形的方法有种．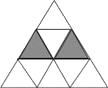
三、解答题：本题共8小题，共66分
-
19. 如图，在正方形网格中，点A，B，C均为网格线交点，请按要求作图，作图过程仅使用无刻度的直尺，保留作图痕迹，无需说明理由．
(1)、如图1，作出关于直线对称的图形；(2)、如图2，在直线上求作点P，使得 ．20. 图1、图2、图3均是的正方形网格，每个小正方形的顶点称为格点，的三个顶点都在格点上．（提醒：①每个小正方形边长1；②所面图中不用标注顶点字母）
(1)、在图1中，画出一个与关于直线AC成轴对称的格点三角形．(2)、在图2中，画出一个与关于直线BC成轴对称的格点三角形．(3)、在图3中，画出一个与面积相等且形状不同的格点三角形．21. 如图，已知的顶点都在格点上，直线l与网线重合（每个小正方形的边长均为1个单位长度）
(1)、画出关于直线l对称的；(2)、将向右平移6个单位长度，再向上平移3个单位长度，得到 ， 画出；(3)、画出绕点A逆时针旋转后得到的 ．22. 如图，将 以点 为旋转中心，顺时针旋转 ，得到 ，过点 作 ，交 的延长线于点 ，求证： ．
23. 如图，点O在直线AB上，射线OC ， OE在与OA重合的位置同时开始绕点O顺时针旋转，OC的旋转速度为每秒2°，OE的旋转速度为每秒6°，当OE与OB重合时停止旋转，在OC的右侧作射线OD使得 ， 设旋转时间为t秒．解答下列问题：
(1)、当秒时，则 ， ；(2)、当的平分线OM与射线OE所组成的时，求旋转时间t ，(3)、是否存在一个常数m ， 使得的值在一定时间范围内不随t的改变而改变？若存在，求出m的值；若不存在，请说明理由．24. 已知两条平行线 ， 和一块含角的直角三角尺 ， 且点E ， F不可能同时落在直线和之间．
(1)、如图①，把三角尺的角的顶点E ， G分别放在 ， 上，若 ， 则的度数为；(2)、如图②，把三角尺的锐角顶点G放在上，且保持不动，若点E恰好落在和之间，且与所夹锐角为 ， 求的度数；(3)、把三角尺的锐角顶点G放在上，且保持不动，旋转三角尺，若存在 ， 求出射线与所夹锐角的度数．