湘教版(2025)数学七年级下册5.2旋转 同步分层练习
试卷日期:2025-04-20 考试类型:同步测试
一、夯实基础
-
1. 有下列现象:①地下水位逐年下降:②传送带的移动;③方向盘的转动:④水龙头开关的转动;⑤钟摆的运动:⑥荡秋千运动。其中属于旋转的有( )A、2个 B、3个 C、4个 D、5个2. 如图,将绕点顺时针旋转到 , 若 , 则( )
 A、 B、 C、 D、3. 如图,△ABC绕点P逆时针旋转一个角度得到△DEF,则下面选项中不能表示旋转角的是( )
A、 B、 C、 D、3. 如图,△ABC绕点P逆时针旋转一个角度得到△DEF,则下面选项中不能表示旋转角的是( ) A、∠CPD B、∠APD C、∠BPE D、∠CPF4. 如图所示,若绕着点逆时针旋转后与重合,那么与线段相等的线段是( )
A、∠CPD B、∠APD C、∠BPE D、∠CPF4. 如图所示,若绕着点逆时针旋转后与重合,那么与线段相等的线段是( ) A、 B、 C、 D、5. 如图,把△ABC绕着点A逆时针旋转40°得到△ADE,∠1=30°,则∠BAE=( )
A、 B、 C、 D、5. 如图,把△ABC绕着点A逆时针旋转40°得到△ADE,∠1=30°,则∠BAE=( ) A、10° B、30° C、40° D、70°6. 将所给木块旋转,能得到下列哪个选项( ).
A、10° B、30° C、40° D、70°6. 将所给木块旋转,能得到下列哪个选项( ). A、
A、 B、
B、 C、
C、 D、
D、 E、
E、 7.
7. (1)、将图中三角形②向( )平移( )格,就正好可以和三角形①拼成一个长方形,画出平移后的三角形。(2)、把三角形③绕点(3,4)沿( )时针方向旋转( )度,可以与三角形①拼成一个平行四边形,并在图中画出旋转后的三角形。8. 按要求画图:
(1)、将图中三角形②向( )平移( )格,就正好可以和三角形①拼成一个长方形,画出平移后的三角形。(2)、把三角形③绕点(3,4)沿( )时针方向旋转( )度,可以与三角形①拼成一个平行四边形,并在图中画出旋转后的三角形。8. 按要求画图: (1)、以直线l为对称轴,画出图①的另一半,使它成为一个轴对称图形;(2)、将图②所示的三角形绕点O顺时针旋转 , 画出旋转后的图形.
(1)、以直线l为对称轴,画出图①的另一半,使它成为一个轴对称图形;(2)、将图②所示的三角形绕点O顺时针旋转 , 画出旋转后的图形.二、能力提升
-
9. 如图,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是 ( )
 A、点M B、点N C、点P D、点Q10. 下列各组图形,只通过平移或旋转,不能形成长方形的是( )A、
A、点M B、点N C、点P D、点Q10. 下列各组图形,只通过平移或旋转,不能形成长方形的是( )A、 B、
B、 C、
C、 D、
D、 11. 把三角形ABC绕点C顺时针方向旋转20°后B落在B'位置,A落在A'位置,且A'B'//BC , 已知∠A=60°,则∠B'CA=( )
11. 把三角形ABC绕点C顺时针方向旋转20°后B落在B'位置,A落在A'位置,且A'B'//BC , 已知∠A=60°,则∠B'CA=( ) A、80° B、60° C、40° D、20°12. 如图,三角形OCD是由三角形OAB绕点O顺时针旋转40°后得到的图形,∠AOB=60°,则∠COB的度数是( )
A、80° B、60° C、40° D、20°12. 如图,三角形OCD是由三角形OAB绕点O顺时针旋转40°后得到的图形,∠AOB=60°,则∠COB的度数是( ) A、60° B、40° C、20° D、10°13. 如图,将绕点C顺时针方向旋转得 , 若 , 则等于( )
A、60° B、40° C、20° D、10°13. 如图,将绕点C顺时针方向旋转得 , 若 , 则等于( ) A、 B、 C、 D、14. 如图,把∠APB放在量角器上,读得射线PA,PB分别经过刻度117和153,把∠APB绕点P按逆时针方向旋转到∠A'PB',当时,射线PA'经过刻度。
A、 B、 C、 D、14. 如图,把∠APB放在量角器上,读得射线PA,PB分别经过刻度117和153,把∠APB绕点P按逆时针方向旋转到∠A'PB',当时,射线PA'经过刻度。 15. 一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使BC边与三角形ADE的一边互相平行.则∠BAD(0°<∠BAD<180°)所有可能符合条件的度数为 .
15. 一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使BC边与三角形ADE的一边互相平行.则∠BAD(0°<∠BAD<180°)所有可能符合条件的度数为 . 16. 两块不同的三角板按如图1所示摆放,AC边与边重合,∠BAC=45°, , 接着如图2保持三角板ABC不动,将三角板绕着点C(点C不动)按顺时针(如图标示方向)旋转,在旋转的过程中,逐渐增大,当第一次等于90°时,停止旋转,在此旋转过程中,=时,三角板有一条边与三角板ABC的边AB恰好平行.
16. 两块不同的三角板按如图1所示摆放,AC边与边重合,∠BAC=45°, , 接着如图2保持三角板ABC不动,将三角板绕着点C(点C不动)按顺时针(如图标示方向)旋转,在旋转的过程中,逐渐增大,当第一次等于90°时,停止旋转,在此旋转过程中,=时,三角板有一条边与三角板ABC的边AB恰好平行. 17. 如图,规定:在网格中每个小格的边长为1个单位长度.作三角形绕点A顺时针旋转,得到三角形 , 点、的对应点为、 . 点在上,旋转后对应点为点 , 连接 .
17. 如图,规定:在网格中每个小格的边长为1个单位长度.作三角形绕点A顺时针旋转,得到三角形 , 点、的对应点为、 . 点在上,旋转后对应点为点 , 连接 . (1)、如图1,三角形绕点A顺时针旋转得到三角形 .
(1)、如图1,三角形绕点A顺时针旋转得到三角形 .①则旋转角为__________;在图中画出点 , 并连接;
②若 , 则___________;
(2)、甲同学发现,在旋转过程中会存在一个时刻,使是的角平分线,如图2,求此时的度数.18. 定义:从一个角的顶点引一条射线,把这个角分成两个角,并且这两个角的度数之比为1:2,这条射线叫做这个角的三分线.显然,一个角的三分线有两条.如图,∠AOB=90°,OC,OD 是∠AOB 的两条三分线,以点 O为中心,将∠COD 顺时针旋转 n°(n < 90) 得到∠C'OD'.当OA 恰好是∠C'OD'的三分线时,求n的值. 19.(1)、利用一副三角板可以画出一些特殊的角,在①135°,②120°,③75°,④50°,⑤35°,⑥15°,四个角中,利用一副三角板画不出来的特殊角是;(填序号)
19.(1)、利用一副三角板可以画出一些特殊的角,在①135°,②120°,③75°,④50°,⑤35°,⑥15°,四个角中,利用一副三角板画不出来的特殊角是;(填序号) (2)、在图①中,写出一组互为补角的两角为;(3)、如图①,先用三角板画出了直线EF , 然后将一副三角板拼接在一起,其中45°角的顶点与60°角的顶点互相重合,且边OA、OC都在直线EF上(图①),固定三角板COD不动,将三角板AOB绕点O按顺时针方向旋转一个角度(如图②),当OB平分时,求旋转角度 .
(2)、在图①中,写出一组互为补角的两角为;(3)、如图①,先用三角板画出了直线EF , 然后将一副三角板拼接在一起,其中45°角的顶点与60°角的顶点互相重合,且边OA、OC都在直线EF上(图①),固定三角板COD不动,将三角板AOB绕点O按顺时针方向旋转一个角度(如图②),当OB平分时,求旋转角度 .三、拓展创新
-
20. 在新型俄罗斯方块游戏中(出现的图案可进行顺时针、逆时针旋转,向左、向右平移),已拼好的图形如图所示.现又出现一个图案正向下运动,若要使该图案与下面的图形拼成一个完整的矩形,则该图案需进行的操作是( )
 A、顺时针旋转 , 向右平移至最右侧 B、逆时针旋转 , 向右平移至最右侧 C、顺时针旋转 , 向左平移至最左侧 D、逆时针旋转 , 向左平移至最左侧21. 如图,现将一副三角尺摆放在一起,重合的顶点为A点,固定含的三角尺不动,将含的三角尺绕顶点A转动,当点E在直线的下方时,使三角尺中的边与三角尺ABC的一边平行,则()可能符合条件的度数为 .
A、顺时针旋转 , 向右平移至最右侧 B、逆时针旋转 , 向右平移至最右侧 C、顺时针旋转 , 向左平移至最左侧 D、逆时针旋转 , 向左平移至最左侧21. 如图,现将一副三角尺摆放在一起,重合的顶点为A点,固定含的三角尺不动,将含的三角尺绕顶点A转动,当点E在直线的下方时,使三角尺中的边与三角尺ABC的一边平行,则()可能符合条件的度数为 . 22. 如图, , , 满足 , 点P是x轴上的一个动点,点C是的中点,连接 , 将绕点C逆时针旋转90°到 .
22. 如图, , , 满足 , 点P是x轴上的一个动点,点C是的中点,连接 , 将绕点C逆时针旋转90°到 . (1)、求A、B、C三点的坐标;(2)、当点P在线段上或延长线上时,若 , 求点E的坐标;(3)、当点P在线段的延长线上时,连接 , 若 , a的值在变化,求点E的运动路径长度.23. 新定义问题
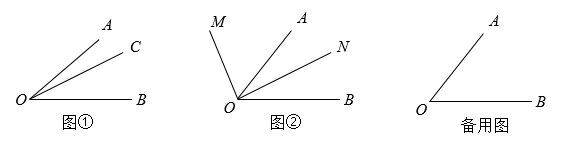
(1)、求A、B、C三点的坐标;(2)、当点P在线段上或延长线上时,若 , 求点E的坐标;(3)、当点P在线段的延长线上时,连接 , 若 , a的值在变化,求点E的运动路径长度.23. 新定义问题如图①,已知 ,在 内部画射线 ,得到三个角,分别为 、 、 .若这三个角中有一个角是另外一个角的2倍,则称射线 为 的“幸运线”.(本题中所研究的角都是大于 而小于 的角.)
 (1)、(阅读理解)
(1)、(阅读理解)角的平分线这个角的“幸运线”;(填“是”或“不是”)
(2)、(初步应用)如图①, ,射线 为 的“幸运线”,则 的度数为;
(3)、(解决问题)如图②,已知 ,射线 从 出发,以每秒 的速度绕 点逆时针旋转,同时,射线 从 出发,以每秒 的速度绕 点逆时针旋转,设运动的时间为 秒( ).若 、 、 三条射线中,一条射线恰好是以另外两条射线为边的角的“幸运线”,求出所有可能的 值.