【培优练】人教版数学八年级下册 18.1.1 平行四边形的性质

试卷日期：2025-04-10 考试类型：单元试卷

前去【出卷网】下载

一、选择题

1. 已知平行四边形 $A B C D$ ，对角线 $A C$ 与 $B D$ 相交于点O，以下表述不一定正确的是（）

A、 $A D ∥ B C$ 且 $A B ∥ C D$ B、 $A B = C D$ 且 $A D = B C$ C、 $A O = C O = B O = D O$ D、 $A B = C D$ 且 $A B ∥ C D$

查看试题解析
2. 在 $▱$ $A B C D$ 中，如果 $∠ A + ∠ C = 4 ∠ B$ ，那么 $∠ B$ 的大小是（）

A、 $45^{\circ}$ B、 $60^{\circ}$ C、 $75^{\circ}$ D、 $90^{\circ}$

查看试题解析
3. 如图，在□ABCD中，AE⊥CD ，垂足为点E ．如果∠B=53°，则∠DAE的度数为（）

A、33° B、37° C、53° D、57°

查看试题解析
4. 如图，在 $▱ A B C D$ 中， $D B = D C$ ， $A E ⊥ B D$ 于点 E，则（）

A、 $∠ B A E + ∠ C = 90 °$ B、 $∠ C - ∠ B A E = 90^{\circ}$ C、 $2 ∠ C - ∠ B A E = 90 °$ D、 $2 ∠ C + ∠ B A E = 180 °$

查看试题解析
5. 如图，在 $▱ A B C D$ 中， $B F$ 平分 $∠ A B C$ ，交 $A D$ 于点F， $C E$ 平分 $∠ B C D$ 交 $A D$ 于点E， $A B = 6, B C = 10$ ，则 $E F$ 长为（　　）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，▱ $A B C D$ 的顶点 $A$ ， $C$ 分别在直线 $E F$ ， $G H$ 上，且 $E F / / G H$ ， $∠ F A D = 26 °$ ，则 $∠ B C G$ 的度数为( )

A、 $34 °$ B、 $24 °$ C、 $30 °$ D、 $26 °$

查看试题解析
7. 如图，平行四边形 $A B C D$ 的周长为 $20 c m$ ， $A B \neq A D$ ， $A C$ 、 $B D$ 相交于点 $O$ ， $E O ⊥ B D$ 交 $A D$ 于点 $E$ ，则 $△ A B E$ 的周长为( )

A、 $8 c m$ B、 $10 c m$ C、 $12 c m$ D、 $20 c m$

查看试题解析
8. 如图，在□ABCD中，对角线AC、BD交于点O ， OE⊥AC ，交AD于点E ，连接CE ．已知△DCE的周长是14，则□ABCD的周长是（）

A、7 B、14 C、28 D、56

查看试题解析
9. 如图，在□ABCD中， $A B = 4$ ， $B C = 6$ ，对角线AC，BD相交于点O，则OA的取值范围是（）

A、 $2 < O A < 10$ B、 $1 < O A < 5$ C、 $4 < O A < 6$ D、 $2 < O A < 8$

查看试题解析
10. 如图所示，在平面直角坐标系中，以A（-1，0），B（2，0），C（0，1）为顶点构造平行四边形，下列各点中不能作为该平行四边形的第4个顶点的坐标的是（）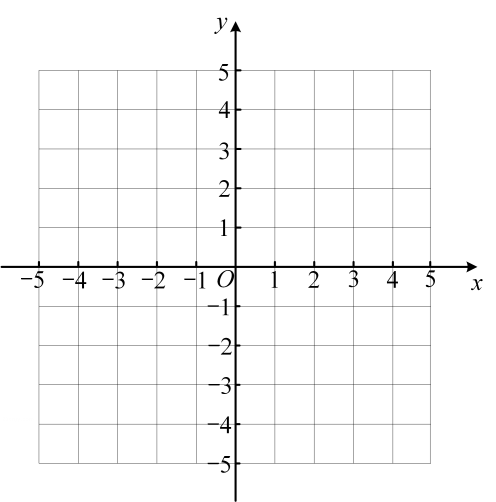

A、（3，1） B、（1，-1） C、（-3，1） D、（-4，1）

查看试题解析
11. 如图，平行四边形ABCD的对角线AC，BD交于点O，AE平分∠BAD，交BC于点E，且∠ADC＝60°， $A B = \frac{1}{2} B C$ ，连接OE，下列结论：①∠CAD＝30°；②OD＝AB；③S_▱ABCD＝AC•CD；④S_{四边形OECD}＝ $\frac{3}{2}$ S_△AOD ，其中成立的个数为（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图，在平行四边形ABCD中，AD＝4，E是边DC延长线上一点，连接BE ，连接FC ，则FC的最小值是（）

A、 $\sqrt{3}$ B、2 C、 $\sqrt{6}$ D、 $2 \sqrt{3}$

查看试题解析

二、填空题

13. 平行四边形的周长为24cm，相邻两边长的比为3：1，那么这个平行四边形较短的边长为 cm．

查看试题解析
14. 在探索数学名题“尺规三等分角”的过程中，有下面的问题：如图，在平行四边形ABCD中，点E是对角线BD上一点，且AB=BE=CE ， ∠A=108°，则∠DBC的大小是．

查看试题解析
15. 如图，在 $▱ A B C D$ 中， $A B = 4$ ， $B C = 6$ ， $A C$ 的垂直平分线交 $A D$ 于点 $E$ ，连接 $C E$ ， $△ C D E$ 的周长为．

查看试题解析
16. 如图， $E$ 是平行四边形ABCD内一点， $△ B C E$ 是正三角形，连结AE，DE，若 $A E ⊥ A D$ ， $D E ⊥ E C$ ，且 $A E = 1, ∠ A D E = 3 0^{°}$ ，则AB的长是．

查看试题解析
17. 在平行四边形 $A B C D$ 中， $A E$ 平分 $∠ B A D$ 交边 $B C$ 于 $E$ ， $D F$ 平分 $∠ A D C$ 交边 $B C$ 于 $F$ .若 $A D = 11$ ， $E F = 5$ ，则 $A B =$ .

查看试题解析
18. 如图，四边形 $A B C D ， A D / / B C ， A B ⊥ B C ， A D = 1 ， A B = 2 ， B C = 3 ， P 为 A B$ 边上的一动点，以 $P D ， P C$ 为边作平行四边形 $P C Q D$ ，则对角线 $P Q$ 的长的最小值是．

查看试题解析

三、解答题

19. 如图，在 $▱ A B C D$ 中，点E是BC边的中点，连接AE并延长与DC的延长线交于点F．

(1)、求证： $C F = C D$ ；

(2)、若 $A D = 13$ ， $A F = 10$ ， $A D = 2 A B$ ，连接DE，求DE的长．

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $B E, D F$ 分别平分 $∠ A B C$ 和 $∠ A D C$ ，交 $A C$ 于点 $E, F$ ．

(1)、求证： $B E = D F$ ；

(2)、过点E作 $E G ⊥ B C$ 于点G ，若 $▱ A B C D$ 的周长为 $36, E G = 4$ ，求 $△ A B C$ 的面积．

查看试题解析
21. 如图，在 $▱ A B C D$ 中，连接 $A C$ ，且 $A C = 2 A B$ ．

(1)、（尺规作图）作出 $∠ B A C$ 的角平分线与 $B C$ 交于点E．连接 $B D$ 交 $A E$ 于点F，交 $A C$ 于点O．

(2)、猜想线段 $B F$ 和线段 $D F$ 的数量关系，并证明你的猜想．

查看试题解析
22. 如图， $▱ A B C D$ 的对角线相交于点 $O$ ，点 $E$ 在边 $B C$ 的延长线上，且 $O E = O B$ ，连结 $D E$ ．

(1)、求证： $D E ⊥ B E$ ．

(2)、设 $C D$ 与 $O E$ 相交于点 $F$ ，若 $O F^{2} + F D^{2} = O E^{2} ， C E = 3 ， D E = 4$ ，求线段 $C F$ 的长．

查看试题解析
23. 如图，在 $□ A B C D$ 中，过点 $C$ 作 $C H ⊥ A B$ 于点 $H$ ，过点 $B$ 作 $A C$ 的垂线，分别交 $C H$ ， $A C ， A D$ 于点 $E ， F ， G$ ，且 $∠ A B C = ∠ B E H ， B G = B C$ ．

(1)、若 $B E = 10 ， B C = 25$ ，求 $D G$ 的长．

(2)、连结 $H F$ ，求证： $H A = \sqrt{2} H F - H E$ ．

查看试题解析
24. 已知平行四边形 $A B C D, E$ 为 $B C$ 边上的中点， $F$ 为 $A B$ 边上的一点．

(1)、如图1，连接 $F E$ 并延长交 $D C$ 的延长线于点 $G$ ，求证： $F E = G E$ ；

(2)、如图2，若 $F B + A B = D F, ∠ E D C = 36 °$ ，求 $∠ A F D$ ；

(3)、如图3，若 $F E = D E, P$ 为 $A F$ 的中点， $Q$ 为 $F D$ 的中点， $A Q = 4, D P = \sqrt{34}$ ，求线段 $B E$ 的长．

查看试题解析