第四章《因式分解》3 公式法（2）—北师大版数学八（下）课堂达标测试

试卷日期：2025-04-05 考试类型：同步测试

前去【出卷网】下载

一、选择题（每题5分，共25分）

1. 下列各式从左到右的变形，因式分解正确的是（）

A、 ${(a + 3)}^{2} = a^{2} + 6 a + 9$ B、 $a^{2} - 4 a + 4 = a (a - 4) + 4$ C、 $a^{2} - 4 a + 4 = {(a - 2)}^{2}$ D、 $5 a x^{2} - 5 a y^{2} = 5 a (x^{2} - y^{2})$

查看试题解析
2. 甲、乙两位同学在对多项式 $x^{2} + b x + c$ 分解因式时，甲看错了 $b$ 的值，分解的结果是 $(x - 4) (x + 5)$ ，乙看错了 $c$ 的值，分解的结果是 $(x + 3) (x - 4)$ ，那么 $c - 5 b$ 的值为（）

A、15 B、 $- 15$ C、25 D、 $- 25$

查看试题解析
3. 把多项式ax³﹣2ax²+ax分解因式，结果正确的是（）

A、ax（x²﹣2x） B、ax²（x﹣2） C、ax（x+1）（x﹣1） D、ax（x﹣1）²

查看试题解析
4. 若多项式 $2 x^{2} + a x - 6$ 能分解成两个一次因式的积，且其中一个次因式 $2 x - 3$ ，则a的值为（）

A、1 B、5 C、 $- 1$ D、 $- 5$

查看试题解析
5. 已知 $2 x - y = 1$ ， $x y = 2$ ，则 $4 x^{3} y - 4 x^{2} y^{2} + x y^{3}$ 的值为（）

A、-2 B、1 C、-1 D、2

查看试题解析

二、填空题（每题5分，共25分）

6. 分解因式： $x y^{2} + 6 x y + 9 x =$ ．

查看试题解析
7. 已知 $a - b = 2 \sqrt{3}$ ， $a b = 1$ ，则 $2 a^{3} b - 4 a^{2} b^{2} + 2 a b^{3} =$ ．

查看试题解析
8. 因式分解： $a x^{2} - 6 a x + 9 a =$ ．

查看试题解析
9. 已知a+b=2，则 $\frac{1}{2}$ a²+ab+ $\frac{1}{2}$ b²=

查看试题解析
10. 如图，四个图形能拼成一个大长方形，据此可写出个多项式的因式分解：．

查看试题解析

三、解答题（共5题，共50分）

11. 分解因式：

(1)、 $2 a^{2} - 18$ ；

(2)、 $x^{2} (2 - y) - (2 - y)$ ．

查看试题解析
12.

(1)、因式分解： $(x + 2) (x + 4) + x^{2} - 4$ ．

(2)、利用因式分解计算： $10 2^{2} + 102 \times 196 + 9 8^{2}$ ．

查看试题解析
13. 学习了乘法公式 ${(a + b)}^{2} = a^{2} \pm 2 a b + b^{2}$ 后，老师向同学们提出了如下问题：
①将多项式 $x^{2} + 4 x + 3$ 因式分解；
① $x^{2} + 4 x + 3$ $= x^{2} + 4 x + 4 - 1$ $= {(x + 2)}^{2} - 1$ $= (x + 3) (x + 1)$ $= (x + 2 + 1) (x + 2 - 1)$
②求多项式 $x^{2} + 4 x + 3$ 的最小值．
②由①，得 $x^{2} + 4 x + 3 = {(x + 2)}^{2} - 1$ ，因为 ${(x + 2)}^{2} \geq 0$ ，所以 ${(x + 2)}^{2} - 1 \geq - 1$ ．所以，当 $x = - 2$ 时， $x^{2} + 4 x + 3$ 的值最小，且最小值为-1．
请你运用上述方法解决下列问题：

(1)、将多项式 $x^{2} + 4 x - 5$ 因式分解；

(2)、求多项式 $m^{2} + 8 m - 6$ 的最小值；

(3)、若多项式 $P = x^{2} - x$ $Q = x - 2$ 比较多项式 $P$ $Q$ 的大小．

查看试题解析
14. 仔细阅读下面例题，解答问题：
例题：已知二次三项式 $x^{2} - 4 x + m$ 有一个因式是 $x + 3$ ，求另一个因式以及m的值．
解：设另一个因式为 $x + n$ ，则 $x^{2} - 4 x + m = (x + 3) (x + n)$ ，
即 $x^{2} - 4 x + m = x^{2} + (n + 3) x + 3 n$ ，
∴ ${\begin{array}{l} n + 3 = - 4 \\ 3 n = m \end{array}$ ，解得 ${\begin{array}{l} m = - 21 \\ n = - 7 \end{array}$ ．
故另一个因式为 $x - 7$ ， m的值为－21．
仿照上面的方法解答下面问题：
已知二次三项式 $x^{2} + 3 x - k$ 有一个因式是x-5，求另一个因式以及k的值．

查看试题解析
15. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、添项拆项法、十字相乘法等等．①分组分解法：将一个多项式适当分组后，可提公因式或运用公式继续分解的方法叫作分组分解法．
例如： $4 x^{2} - 4 x - y^{2} + 1 = (4 x^{2} - 4 x + 1) - y^{2} = {(2 x - 1)}^{2} - y^{2} = (2 x - y - 1) (2 x + y - 1)$

②十字相乘法：十字相乘法能用于二次三项式的分解因式．

分解步骤：1．分解二次项，所得结果分别写在十字交叉线的左上角和左下角；2．分解常数项，所得结果分别写在十字交叉线的右上角和右下角；3．交叉相乘，求代数和，使其等于一次项；4．观察得出原二次三项式的两个因式，并表示出分解结果．这种分解方法叫作十字相乘法．

例如： $x^{2} - 3 x - 40$ 分析： $x^{2} - 3 x - 40$

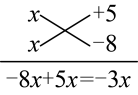
观察得出：两个因式分别为 $(x + 5)$ 与 $(x - 8)$

解：原式 $= (x + 5) (x - 8)$

③添项拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法叫作拆项法．

例如： $y^{2} - 10 y + 21 = y^{2} - 10 y + 25 - 4 = {(y - 5)}^{2} - 2^{2} = (y - 5 + 2) (y - 5 - 2) = (y - 3) (y - 7)$ ．

(1)、仿照以上方法，按照要求分解因式：
①（分组分解法） $a b - a - b + 1 =$ ；
②（十字相乘法） $y^{2} + 3 y - 10 =$ ；

(2)、已知：a、b、c为 $△ A B C$ 的三条边， $a^{2} + b^{2} + c^{2} - 6 a = 10 b + 8 c - 50$ ，判断 $△ A B C$ 的形状．

查看试题解析

第四章 《因式分解》3 公式法（2）—北师大版数学八（下） 课堂达标测试

一、选择题（每题5分，共25分）

二、填空题（每题5分，共25分）

三、解答题（共5题，共50分）

第四章《因式分解》3 公式法（2）—北师大版数学八（下）课堂达标测试